Предмет: Алгебра,
автор: potapov4740982
Помогите найти производную функции
Приложения:
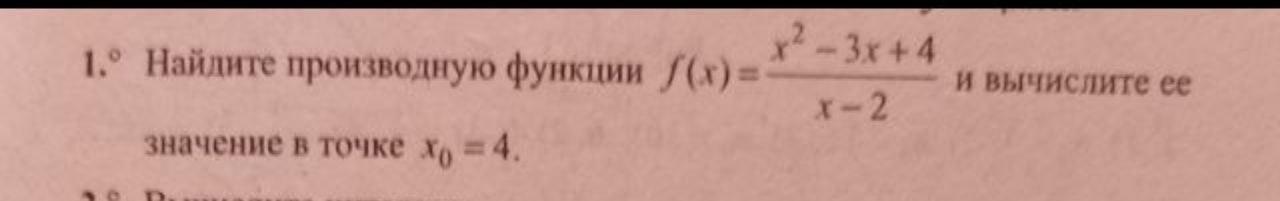
Ответы
Автор ответа:
1
Найти производную функции и вычислить ее значение в точке x₀ = 4.
Решение:
Похожие вопросы
Предмет: Українська мова,
автор: Фангелина
Предмет: Русский язык,
автор: innaindigo
Предмет: Русский язык,
автор: defoos
Предмет: Математика,
автор: Dron066