Предмет: Алгебра,
автор: swetlanaprya
Помогите решить логарифмическое уравнение (номер 819)
P.S решение с другого примера (так нужно;))
Приложения:
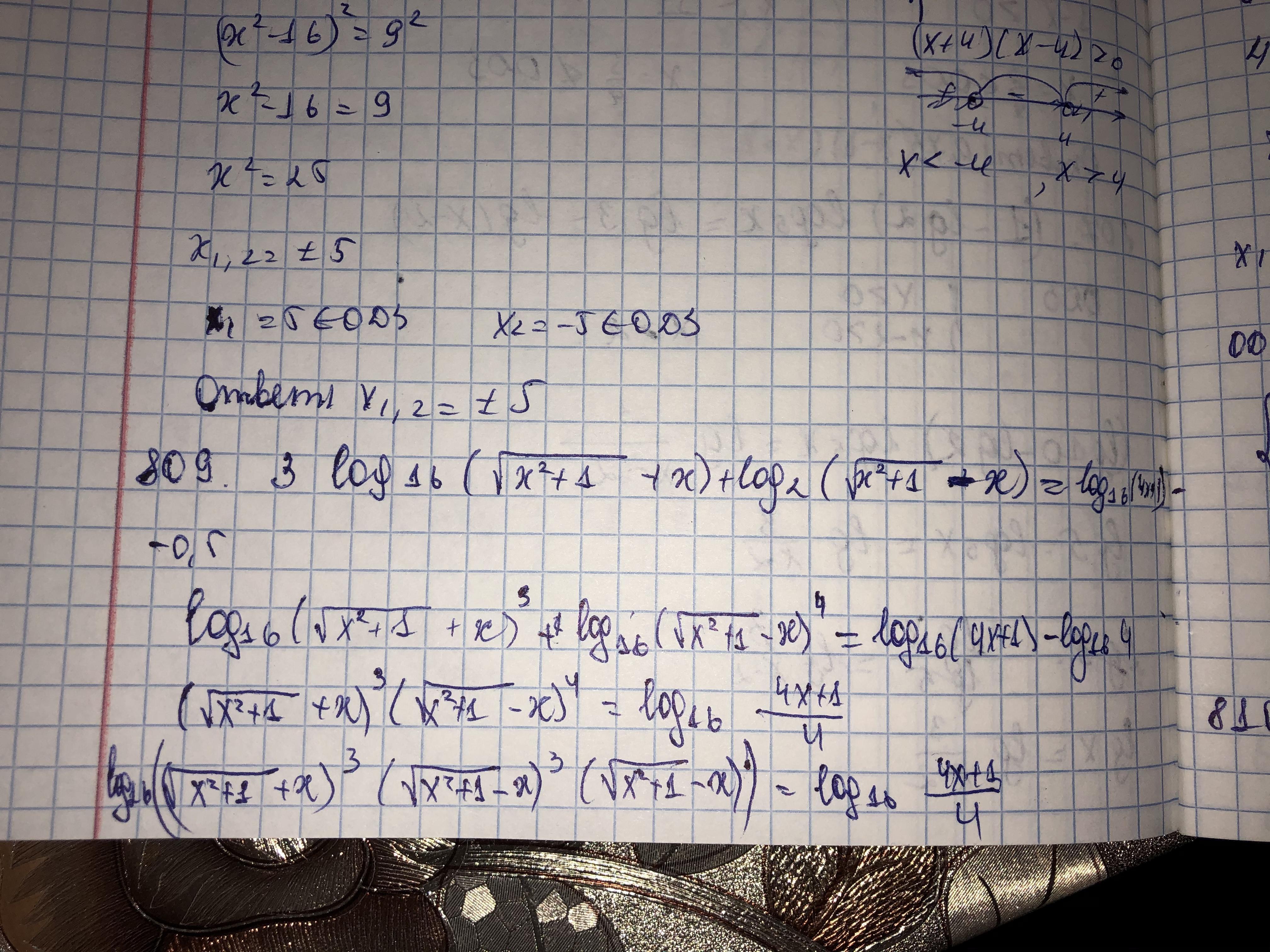

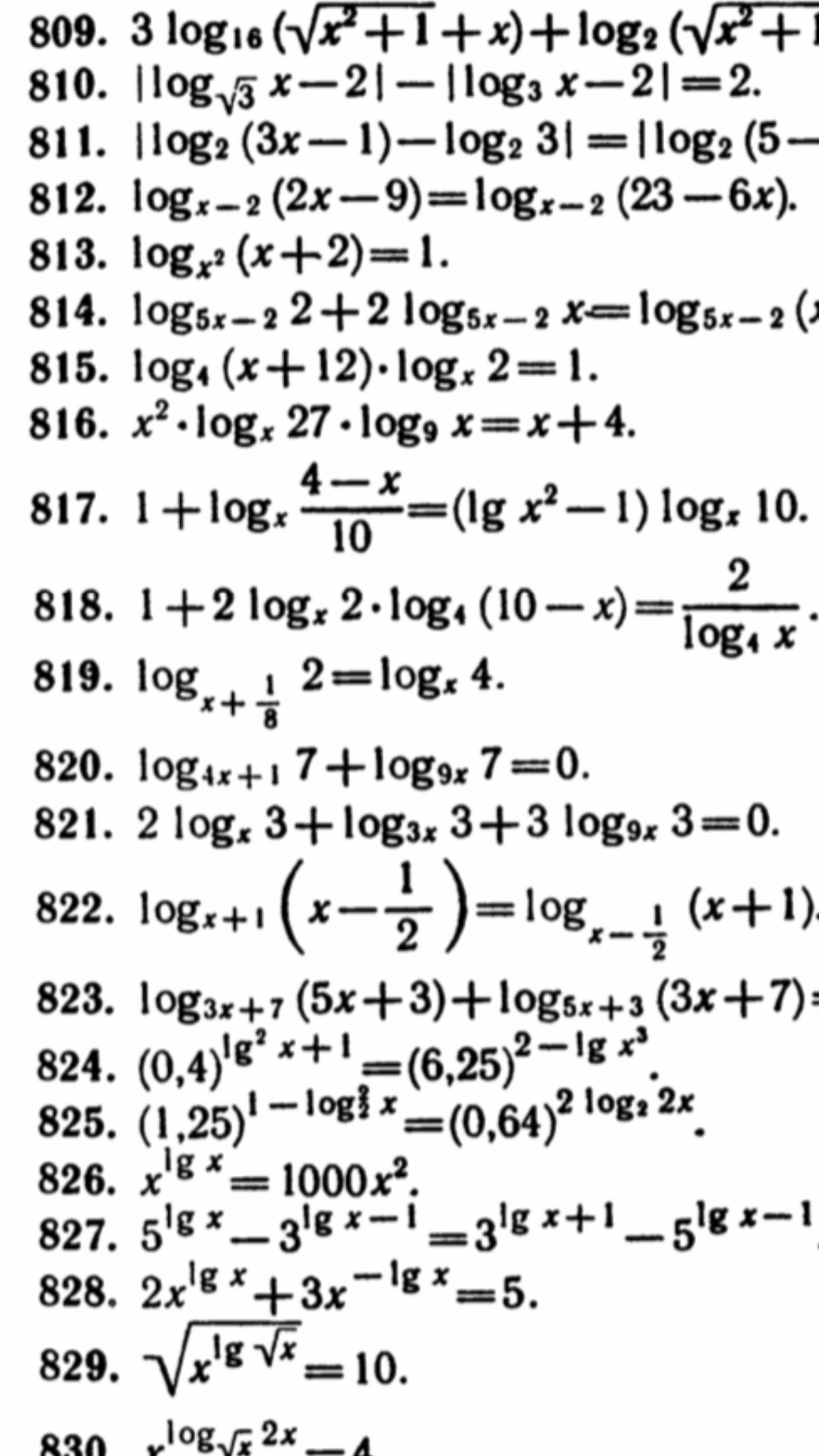
swetlanaprya:
Задание изменилось!!! С тем я разобралась
Ответы
Автор ответа:
0
Теперь выпишем все ограничения на x:
Очевидно, что оба корня подходят.
Ответ:
В дискриминанте «минус 1/4», а так суть решения верна. Я поняла, спасибо тебе огромное ещё раз)
Ой, минус 1/16
Исправил) Спасибо.
И там будет два корня, так как 3-2 корней из 2 положительное число
Действительно. Что-то ночью плохо думается))
Вот именно! Я уже не могу решать эти уравнения. А их ещё много(((
Раньше надо было решать))
Ахаххахахаха, реально
Похожие вопросы
Предмет: Английский язык,
автор: ShabanovaKs
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: AfricanAmerican
Предмет: История,
автор: ютубер7
Предмет: Литература,
автор: Terya228