Предмет: Алгебра,
автор: Setemark
Нужна помощь!!!!!
1) cosXcosП/6+sinXsinП/6<=1/2
2) система:
Х+у=П
SinX+SinY=1
Приложения:
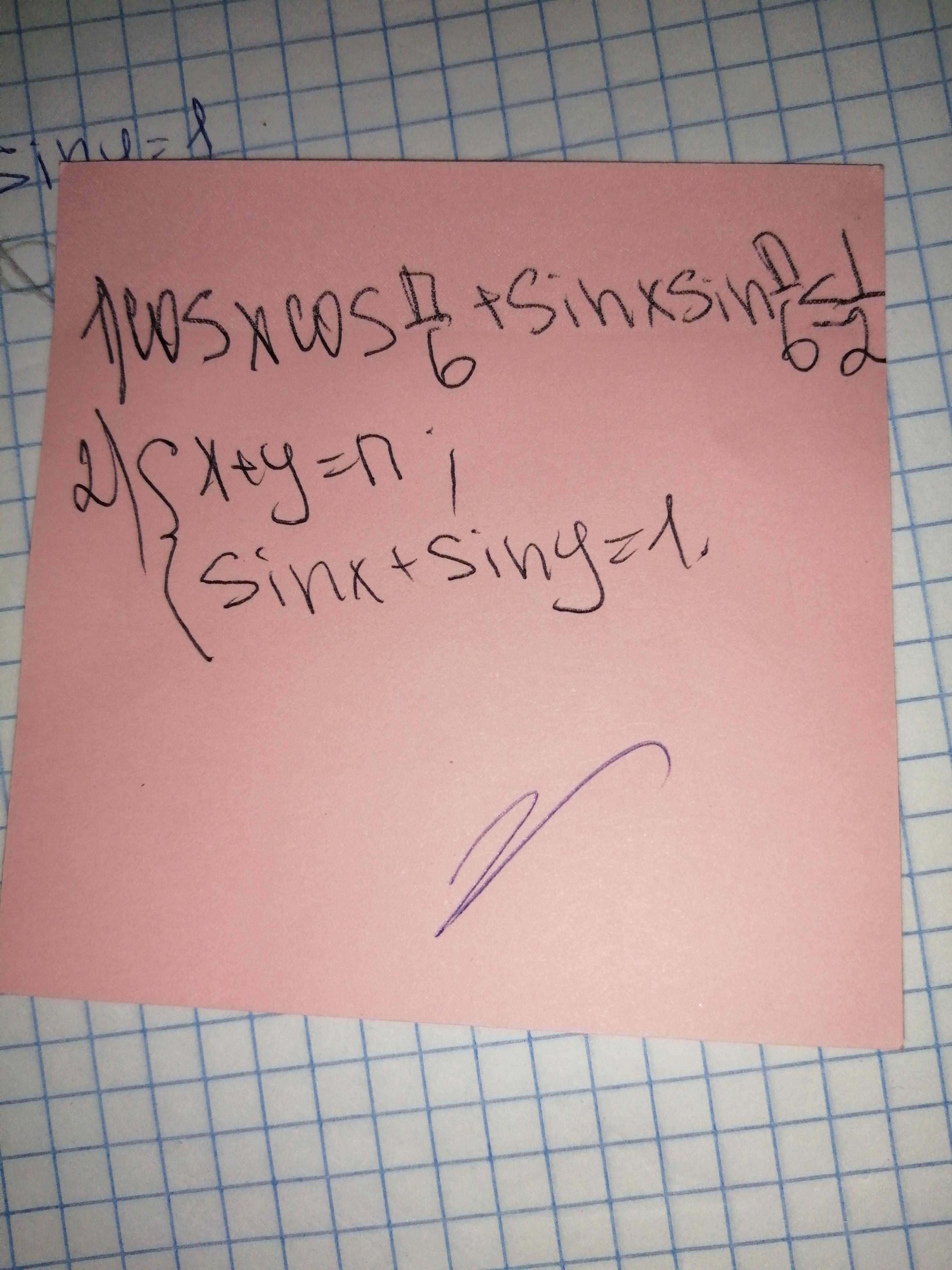
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: msinichkina
Предмет: Русский язык,
автор: m08
Предмет: Русский язык,
автор: nnv150581
Предмет: Литература,
автор: Natavol5
Предмет: Математика,
автор: ангел639