Предмет: Математика,
автор: vvalleraa
Представить в тригонометрической форме числа(50Б)
Приложения:
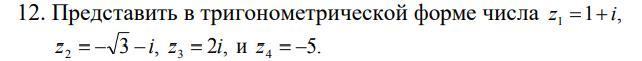
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
для z = a + bi => z = |z|*(cos(α) + i*sin(α))
поэтому:
1) |z| = √(1^2 + 1^2) = √2
α = arctg(b/a) = arctg 1 = /4
z = √2 * (cos(/4) + i*sin(
/4))
2) |z| = √((-3)^2 + (-1)^2) = √10
α = arctg(b/a) = arctg √3 = /3
z = √10 * (cos(/3) + i*sin(
/3))
3) |z| = √((0)^2 + (2)^2) = 2
α = arctg(b/a) = arctg ∞ (грубо т.к. на самом деле 2/0 это неопределенность) = /2
z = 2 * (cos(/2) + i*sin(
/2))
4) |z| = √((-5)^2 + (0)^2) = 5
α = arctg(b/a) = arctg 0 = 0
z = √10 * (cos(0) + i*sin(0))
Похожие вопросы
Предмет: Английский язык,
автор: Алиса483
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Kaite22
Предмет: Физика,
автор: sparta134rus
Предмет: Математика,
автор: vanyaaa825