Предмет: Алгебра,
автор: ellen0004812
СРОЧНО
Найти значение выражения:
cos(pi/4-B)-cos(pi/4-B) если sin B = 1
Приложения:
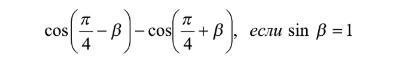
LuciferMotningstar:
еще надо?
Ответы
Автор ответа:
151
Похожие вопросы
Предмет: Русский язык,
автор: kobra525
Предмет: Русский язык,
автор: mvf1705
Предмет: Русский язык,
автор: alina66666677777
Предмет: Химия,
автор: Kaktusik18
Предмет: Литература,
автор: sashantit