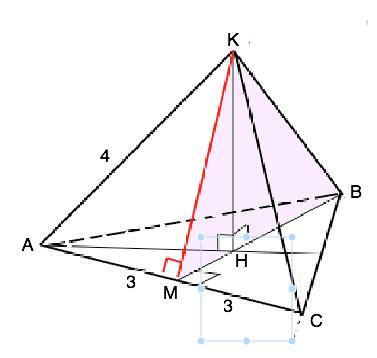
Сторона основания правильной треугольной пирамиды равна 6 м, а боковое ребро — 4 м. Найдите площадь сечения, проходящего через боковое ребро и высоту пирамиды.
Ответы
Ответ: Ѕ=3√3 м²
Объяснение: В правильной треугольной пирамиде основанием является правильный треугольник, а вершина проецируется в центр основания.
Обозначим основание пирамиды АВС, её вершину К. проекцию вершины на основание- Н, апофему на грани АКС - КМ.
Искомое сечение - КВМ, которое содержит высоту пирамиды КН, перпендикулярную основанию, ⇒ плоскость ∆ КВМ перпендикулярна АВС, а ВМ и КМ перпендикулярны АС по т.о 3-х перпендикулярах.
КВМ - треугольник. Формула площади треугольника
S=h•a•1/2, где а - сторона треугольника, h- высота, проведенная к ней.
Ѕ(КВМ)=KH•ВМ/2
Все стороны основания равны 6, углы -60°
ВМ=ВС•sin60°=3√3
По т.Пифагора апофема KM=√(AK²-AM²)=√(16-9)=√7
Высоты правильного треугольника - медианы и точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ МН=ВМ:3=√3
По т.Пифагора KH=√(KM²-MH²)=√(7-3)=√4=2
S(KBM)=3√3•2•1/2=3√3 м²