Предмет: Геометрия,
автор: Eliza0505
знайдіть радіус кола описаного навколо трикутника зі сторонами 30 см, 26 см та 8 см
Ответы
Автор ответа:
21
Дано :
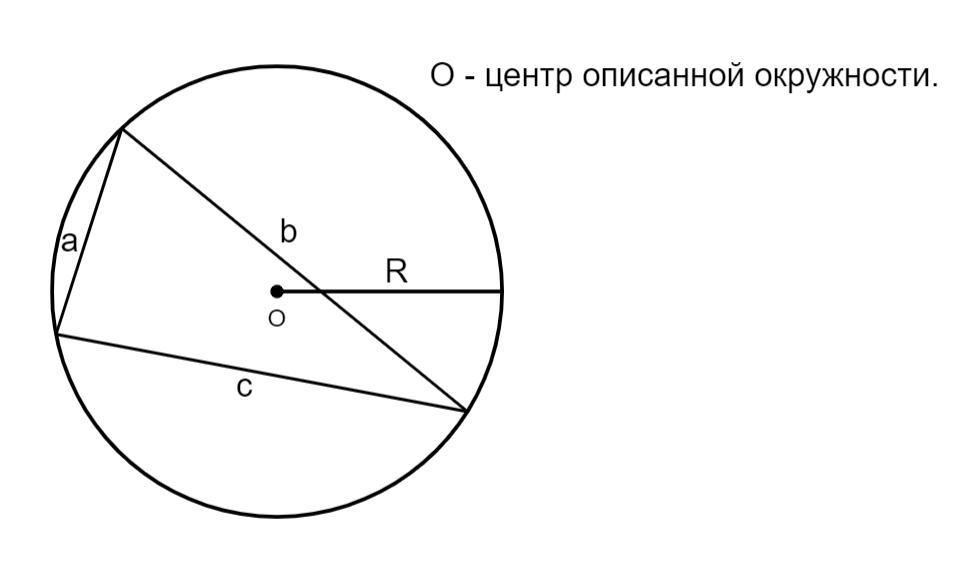
a, b, c - стороны треугольника ; R - радиус описанной около треугольника окружности.
а = 8 см, b = 30 см, c = 26 см.
Найти :
R = ?
Решение :
Найдём площадь треугольника по формуле Герона -
, где p - полупериметр.
(см).
(см²).
Найдём радиус описанной окружности -
(см).
Ответ :
16,25 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: злата16
Предмет: Русский язык,
автор: vickusick
Предмет: Русский язык,
автор: djcgbnfntkm
Предмет: Биология,
автор: ислам311
Предмет: Математика,
автор: Аноним