Предмет: Алгебра,
автор: vikibogatir
Решить систему уравнений способом сложения.
Расписать всё детально,если можно)
Приложения:
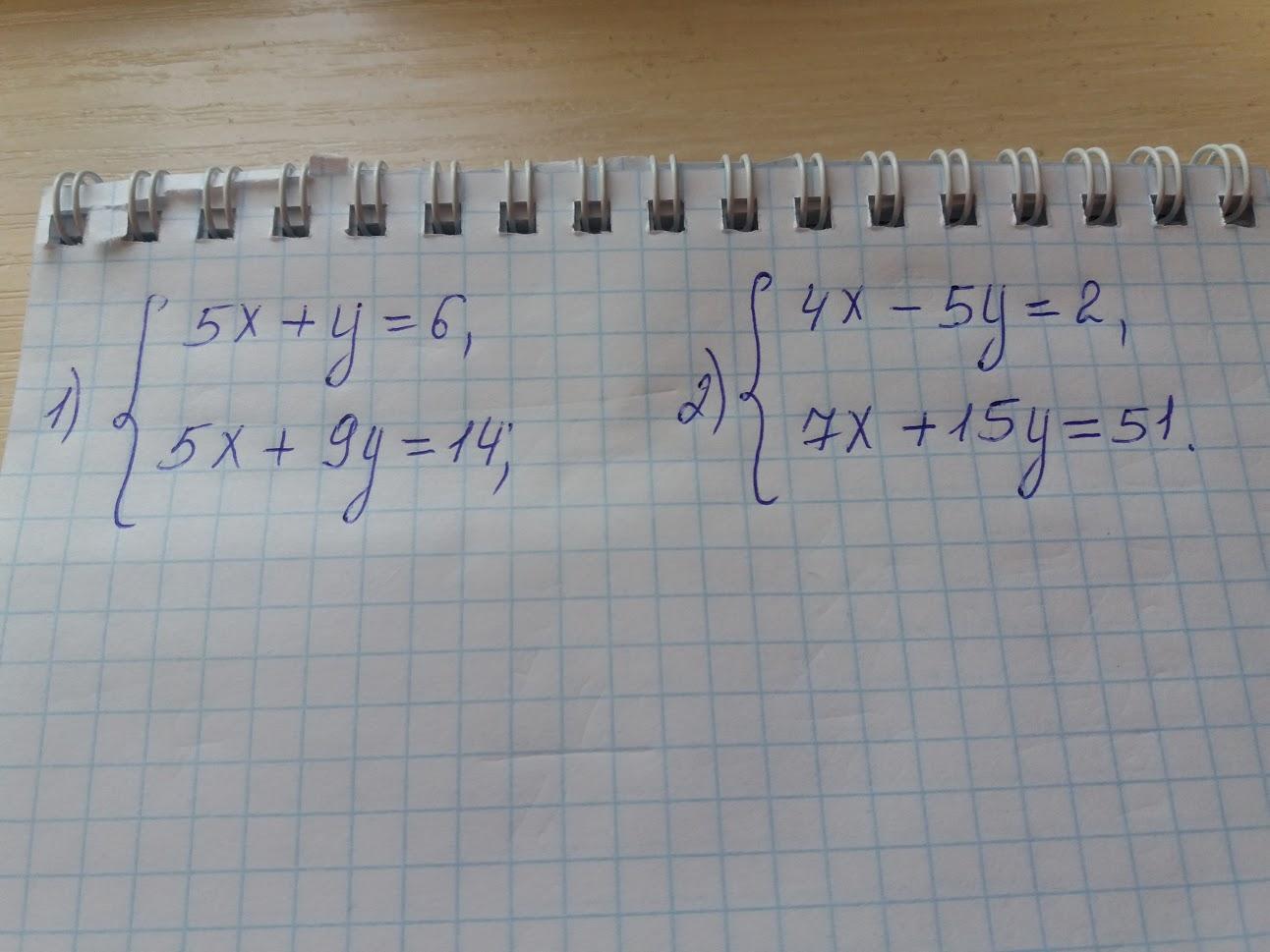
Ответы
Автор ответа:
0
Ответ:
1) (1 ; 1)
2) (3 ; 2)
Решение во вложении ↓
Приложения:

Автор ответа:
0
Умножаем первое уравнение системы на (-1):
Сложим почленно первое и второе уравнения системы, тем самым, исключим неизвестное х. Полученный результат сложения уравнений запишем как первое уравнение новой системы. Вторым уравнением запишем наиболее простое уравнение из условия задания:
Находим значение у и подставим его во второе уравнение для нахождения значения х:
Ответ: (1; 1).
Умножаем первое уравнение системы на 3:
Сложим почленно два уравнения:
Ответ: (3; 2).
Похожие вопросы
Предмет: Другие предметы,
автор: Кремовая
Предмет: Русский язык,
автор: ученик27
Предмет: Русский язык,
автор: swik
Предмет: Биология,
автор: Hulimysara
Предмет: Математика,
автор: Pro100sofya