Предмет: Алгебра,
автор: 1telibaeva
1/х<=х/х+6
Хелп срочно
Ответы
Автор ответа:
1
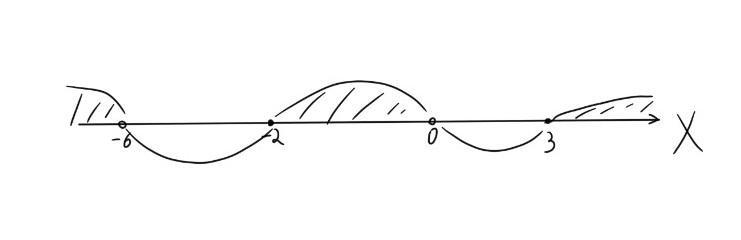
Решаем последнее неравенство методом интервалов (рисунок приложен)
Ответ:
Приложения:
1telibaeva:
Спасибо большое
На здоровье)
Похожие вопросы
Предмет: Другие предметы,
автор: annakovnatska
Предмет: Українська мова,
автор: MashaShatna
Предмет: Русский язык,
автор: kajjgorodovaj
Предмет: Биология,
автор: iragrigorian20
Предмет: Математика,
автор: анкея