Question

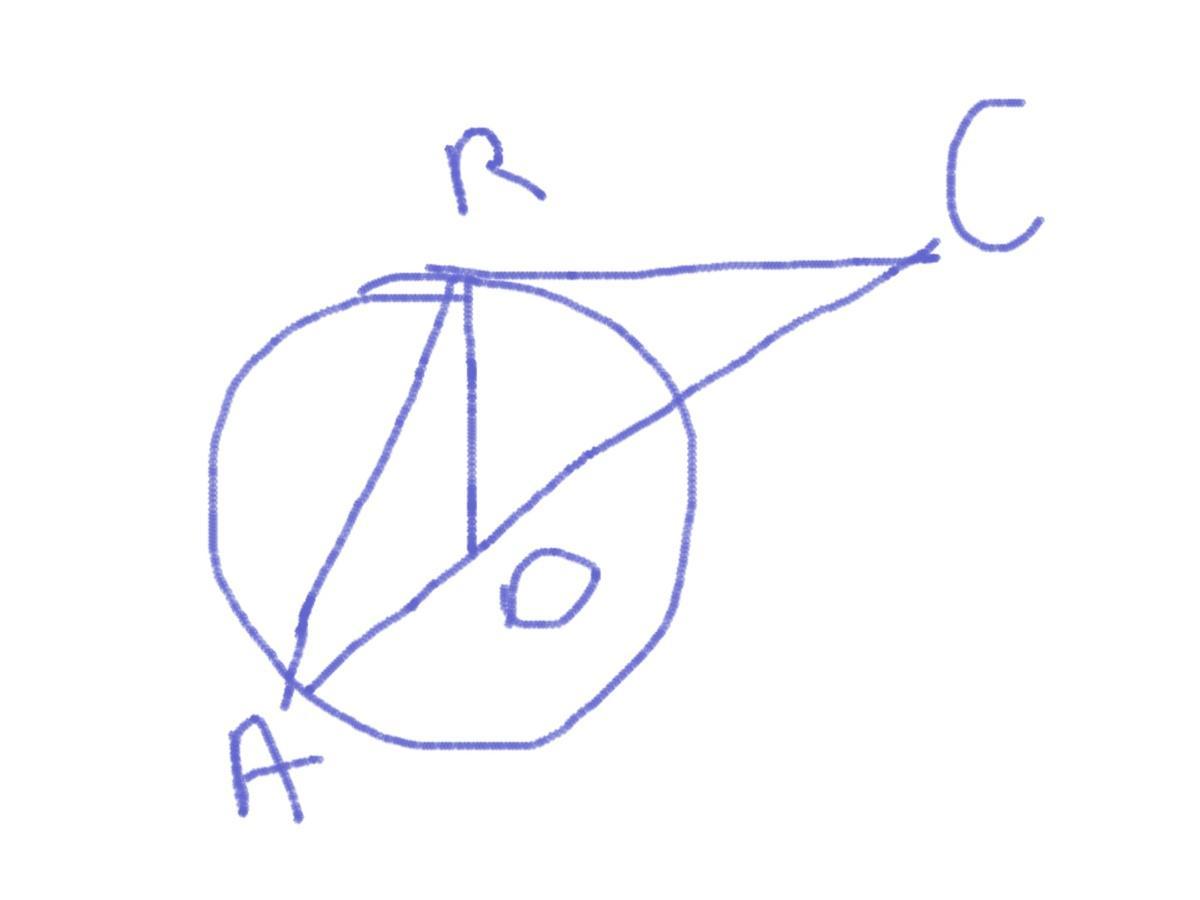
на рисунке 111 точка о центр окружности BC касательная к окружности BCA 20 градусов найти угол BAC

Answer 1

Дано:

т. O — центр окружности

BC — касательная

∠BCA = 20°

Найти:

∠BAC

                                                Решение:

Радиус окружности, проведенный в точку касания, перпендикулярен касательной. Это значит, что OB ⊥ BC и ∠OBC = 90°.

Рассмотрим прямоугольный треугольник OBC.

Сумма острых углов прямоугольного треугольника равна 90°, значит:

∠BOC = 90° - ∠BCA = 90 - 20 = 70°.

∠BOC является центральным углом, поскольку его вершиной является центр окружности.

А искомый ∠BAC является вписанным углом, поскольку его вершина лежит на данной окружности.

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и он, поэтому:

∠BAC = ∠BOC : 2 = 70 : 2 = 35°.

Ответ: 35°.