Предмет: Алгебра,
автор: dimonyes123
Помогите пожалуйста с алгеброй
Приложения:
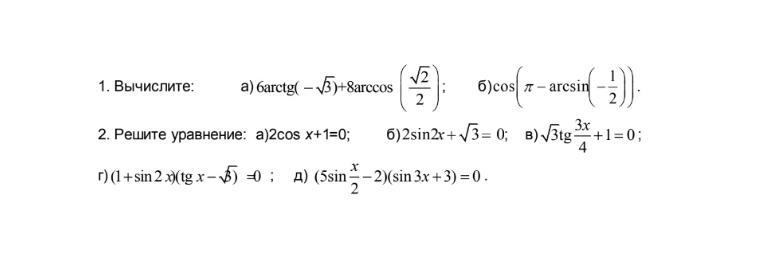
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Mitsuki
Предмет: Русский язык,
автор: kissula2001
Предмет: Русский язык,
автор: elusik
Предмет: Математика,
автор: 87771751045
Предмет: Биология,
автор: toijyiomtuyi