Question

Диаметр окружности равен 8 см. Около неё описана равнобедренная трапеция, боковая сторона которой 10 см.
Вычисли основания и площадь трапеции.

Меньшее основание трапеции равно
см,
большее основание равно
см,
площадь трапеции равна
см2.

Answer 1

Ответ:

4 см,  16 см,  80 см²

Объяснение:

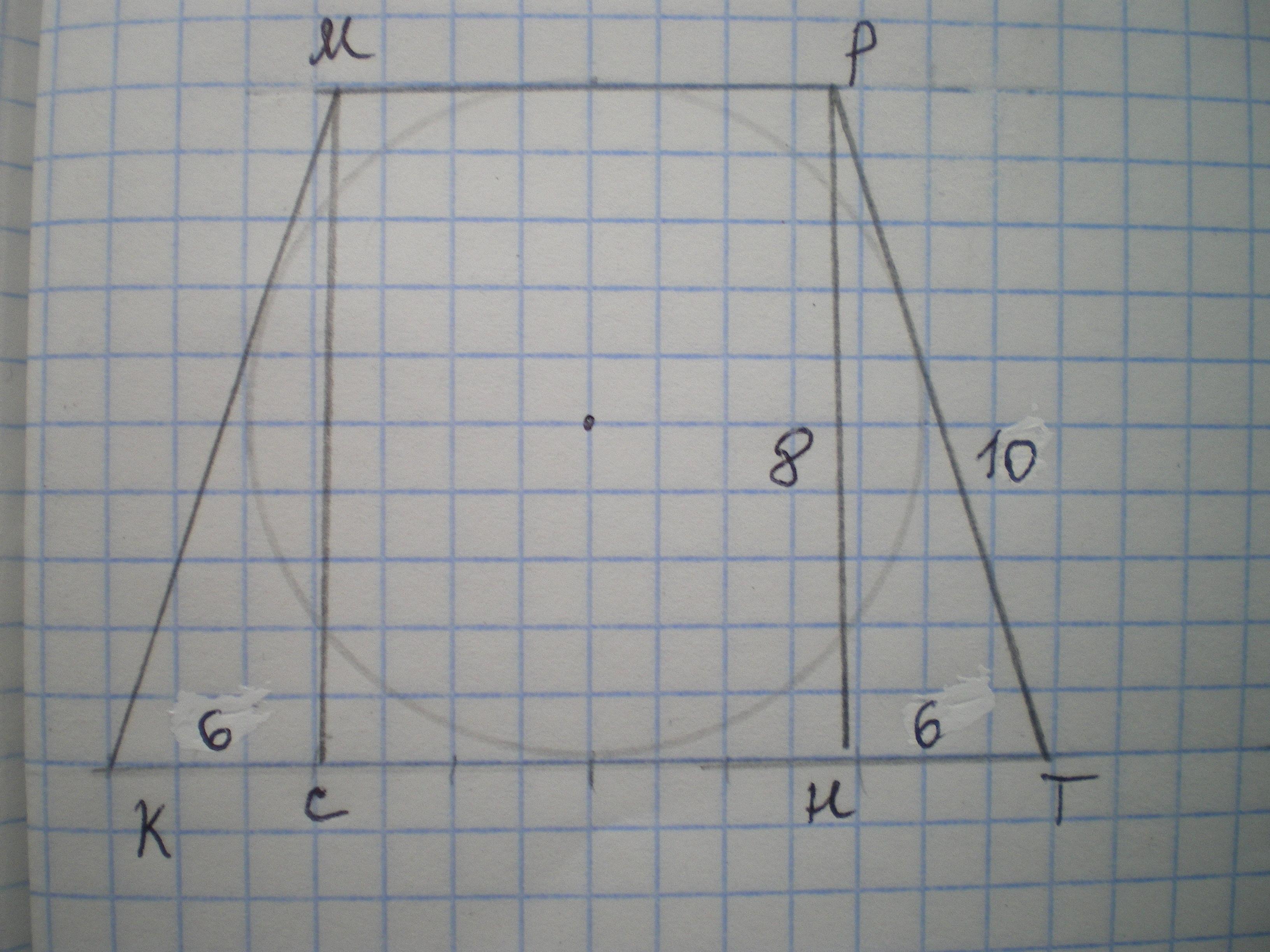
Если вокруг трапеции можно описать окружность, значит сумма боковых сторон равна сумме оснований трапеции. По условию КМ=РТ=10 см,  КМ+РТ=МР+КТ=10+10=20 см.. Высота РН=D=8 см

S=(КМ+РТ):2*РН=20:2*8=80 см²

Проведем высоту МС=РН=8 см.

ΔКМС=ΔТРН по катету и гипотенузе, поэтому КС=ТН

Найдем ТН по теореме Пифагора

ТН=√(РТ²-РН²)=√(100-64)=√36=6 см.

КС+ТН=6+6=12 см

Пусть МР=х см, тогда КТ=х+12 см

х+х+12=20;  2х+12=20;  2х=8;  х=4.

МР=4 см,  КТ=4+12=16 см.