Question

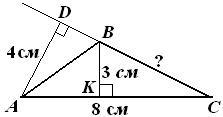
Найдите сторону ВС треугольника АВС, изображенного на рисунке. Задача на площадь треугольника

Answer 1

Дано:

AD = 4 см.

BK = 3 см.

AC = 8 см.

△ADC и BKC - прямоугольные.

Найти:

Если в прямоугольном треугольнике катет равен половине гипотенузы, то напротив лежащий угол равен 30°.

=> ∠C = 30°.

Сумма острых углов прямоугольного треугольника равна 90°.

=> ∠DAC = 90˚ - 30˚ = 60˚.

Если угол прямоугольного треугольника равен 60°, то противолежащий катет равен произведению меньшего катета на √3.

=> DC = 4√3 см.

S △АВС = 1/2АС * ВК = 8/2 * 3 = 12 см²

S △ADC = AD * DC/2 = 4 * 4√3/2 = 8√3 см²

=> S △ADB = S △ADC - S △ABC = 8√3 - 12 = 4(2√3 - 3) см²

Составим уравнение:

Пусть х - DB.

S △ADB = AD * DB/2

4(2√3 - 3) = 4 * x/2

8√3 - 12 = 2x

2x = 8√3 - 12

x = 4√3 - 6

Итак, если DB = (4√3 - 6) см и DC = 4√3 см, то ВС = 6 см.

Ответ: 6 см.