Предмет: Геометрия,
автор: agent9920
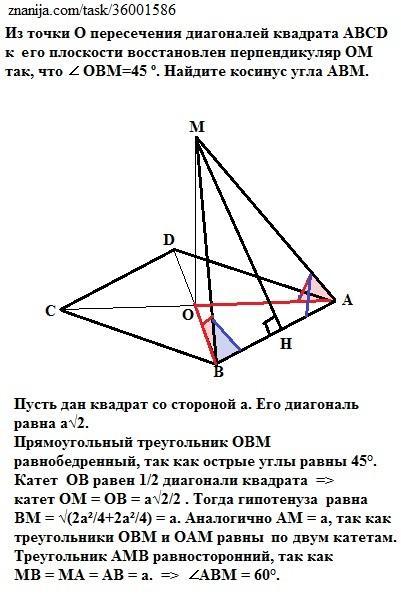
Из точки О пересечения диагоналей квадрата АВСD к е го плоскости восстановлен перпендикуляр ОМ так, что ∠ ОВМ=45 º. Найдите косинус угла АВМ.
Ответы
Автор ответа:
4
Ответ:
∠АВМ = 60°.
Объяснение:
Пусть дан квадрат со стороной а. Его диагональ равна а√2.
Прямоугольный треугольник ОВМ равнобедренный, так как острые углы равны 45°.
Катет ОВ равен 1/2 диагонали квадрата =>
катет ОМ = ОВ = а√2/2 . Тогда гипотенуза равна
ВМ = √(2а²/4+2а²/4) = а.
Аналогично АМ = а, так как треугольники ОВМ и ОАМ равны по двум катетам. Треугольник АМВ равносторонний, так как
МВ = МА = АВ = а. => ∠АВМ = 60°.
Приложения:
agent9920:
я вижу что это всё правильно но в ответе должно получиться 0.5 не подскажите как это?
Похожие вопросы
Предмет: Английский язык,
автор: манюньчик04
Предмет: Русский язык,
автор: Ириска81
Предмет: Русский язык,
автор: Dank12
Предмет: Физика,
автор: igor000111213
Предмет: География,
автор: Dmitriev228