Предмет: Математика,
автор: Fedorleto
Найдите общее решение дифференциального уравнения. Решения с сайтов не подойдут. Нужно подробнее.
Приложения:
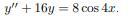
Ответы
Автор ответа:
1
- ЛНДУ 2 пор.
1) Лин. однородное дифф.уравнение 2 пор. : .
Характеристическое уравнение:
Общее решение ЛОДУ 2 пор. :
2) Вид частного решения ЛНДУ 2 пор. :
Частное решение ЛНДУ 2 пор. :
Общее решение ЛНДУ 2 порядка имеет вид :
Общее решение ЛНДУ 2 порядка :
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: gromova7979
Предмет: Математика,
автор: настя355пораоо
Предмет: Физика,
автор: DenisOrlov68