Предмет: Алгебра,
автор: krytayacchiksa
Решите пожалуйста пример прошу
Приложения:
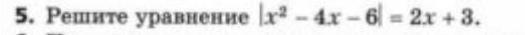
Ответы
Автор ответа:
3
Похожие вопросы
Предмет: Английский язык,
автор: denrey619
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: anilafrunza
Предмет: Математика,
автор: orenart2010
Предмет: История,
автор: каринка0055