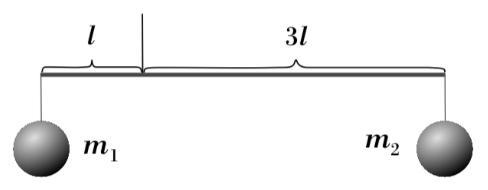
К тросу подъемного крана прикреплен лёгкий рычаг с двумя грузами одинакового объема, как показано на рисунке. Рычаг сбалансирован. Кран опускает грузы в воду таким образом, что рычаг находится над ее поверхностью, а грузы полностью погружены. В результате баланс рычага нарушается. Рабочий встает на тот конец рычага, который начал приподниматься, и рычаг возвращается в равновесное горизонтальное положение. Определите, на сколько изменилась сила натяжения троса по сравнению с начальным значением. Ответ выразите в Н, округлив до целого числа. Масса рабочего составляет 60 кг, плотность воды 1000 кг/м3, ускорение свободного падения 10 Н/кг, масса груза m1=500 кг, длина меньшего плеча рычага l=0,5 м.
Ответы
Ответ:
Объяснение:
m=60 кг
p= 1000 кг/м^3
g= 10 Н/кг
m1=500 кг
L1=0,5 м.
L2=3*L
V1=V2
ΔT=?
F1=m1*g = 500*10 = 5000 H
по правилу моментов
F1*L1=F2*L2
F2=F1*L1 / L2 =F1*L1 / 3*L1 = F1 / 3 = 5000/3=1666.7 H
плотность второго груза меньше первого в 3 раза.
Тогда натяжение троса в воздухе
Т1 = F1+F2 = 5000+1666.7 == 6667 H
при погружении в воду
(F1 - p*g*V)*L1 = (F2 - p*g*V +m*g)*L2
F1 - p*g*V = (F2 - p*g*V +m*g)*3
F1 - p*g*V = 3*F2 - 3*p*g*V +3*m*g
5000 - 10*1000*V = 3*1666.7 - 3*1000*10*V +3*60*10
5000 -10000*V = 5000 - 30000*V +1800
-10*V = - 30*V +1.8
20V = 1.8
отсюда объем
V=0.09 м^3
найдем архимедову силу
Fa=p*g*V = 1000*10*0.09 = 900 Н
найдем натяжение когда грузы в воде
T2=(F1 - Fa) + (F2+m*g - Fa) = (5000-900) + (1667+60*10-900) ==5467 H
найдем разность натяжений
ΔT = T1-T2 = 6667 - 5467 = 1200 Hьютон