Предмет: Геометрия,
автор: 1904bkp6m4j0
Площадь прямоугольного треугольника равна 722 и 3 под корнем.Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла
Ответы
Автор ответа:
1
Держи братик
Пусть катет лежащий против угла в 30 градусов х, тогда гипотенуза прямоугольного треугольника 2х.
По теореме Пифагора найдем второй катет:
4х^2-х^2=у^2
у^2=3х^2
у=х корней из 3
Так же дано, что площадь равна 722 корня из 3.
Площадь в прямоугольном треугольнике можно найти через полупроизведение катетов:
S=(x*x корней из 3)/2=722 корня из 3
x^2/2=722
x^2=1444
x=38
Катет лежащий против угла в 30 градусов равен 38.
Ответ: 38.
Автор ответа:
0
Пусть АВ = х, тогда ВС = 2х и АС = х√3 . (По теореме Пифагора)
Площадь прямоугольного треугольника равна половине произведения его катетов.
х^2√3 = 1444√3
х^2 = 1444
х = 38
Ответ : 38.
Приложения:
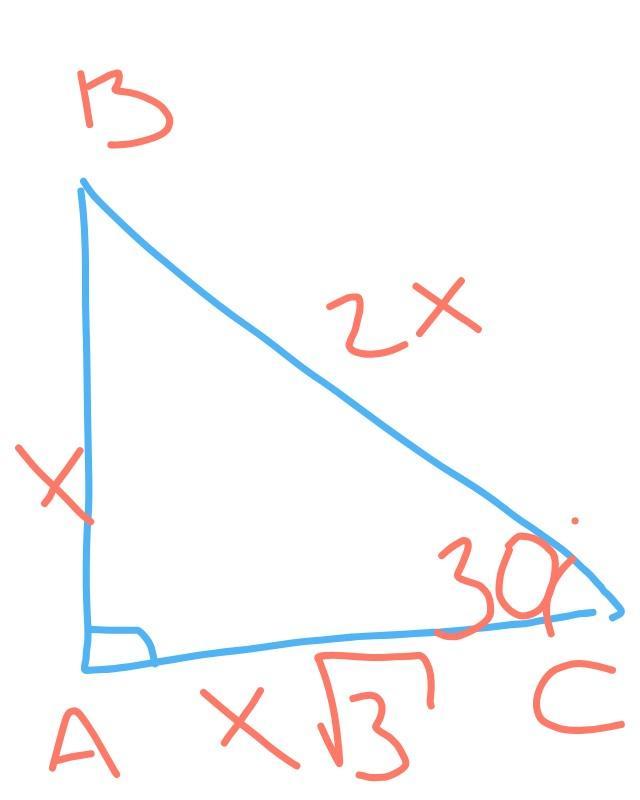
Похожие вопросы
Предмет: Русский язык,
автор: катько1356
Предмет: Русский язык,
автор: ttttll
Предмет: Қазақ тiлi,
автор: timson2002
Предмет: Физика,
автор: vikaromaha2
Предмет: Математика,
автор: Dilmurod777