Предмет: Алгебра,
автор: qrty03
Решить систему уравнений
x^2-y^2=3
x^2+y^2=5
Ответы
Автор ответа:
2
Автор ответа:
1
Ответ:
Вот решение. Возникнут вопросы напиши
Объяснение:
Приложения:
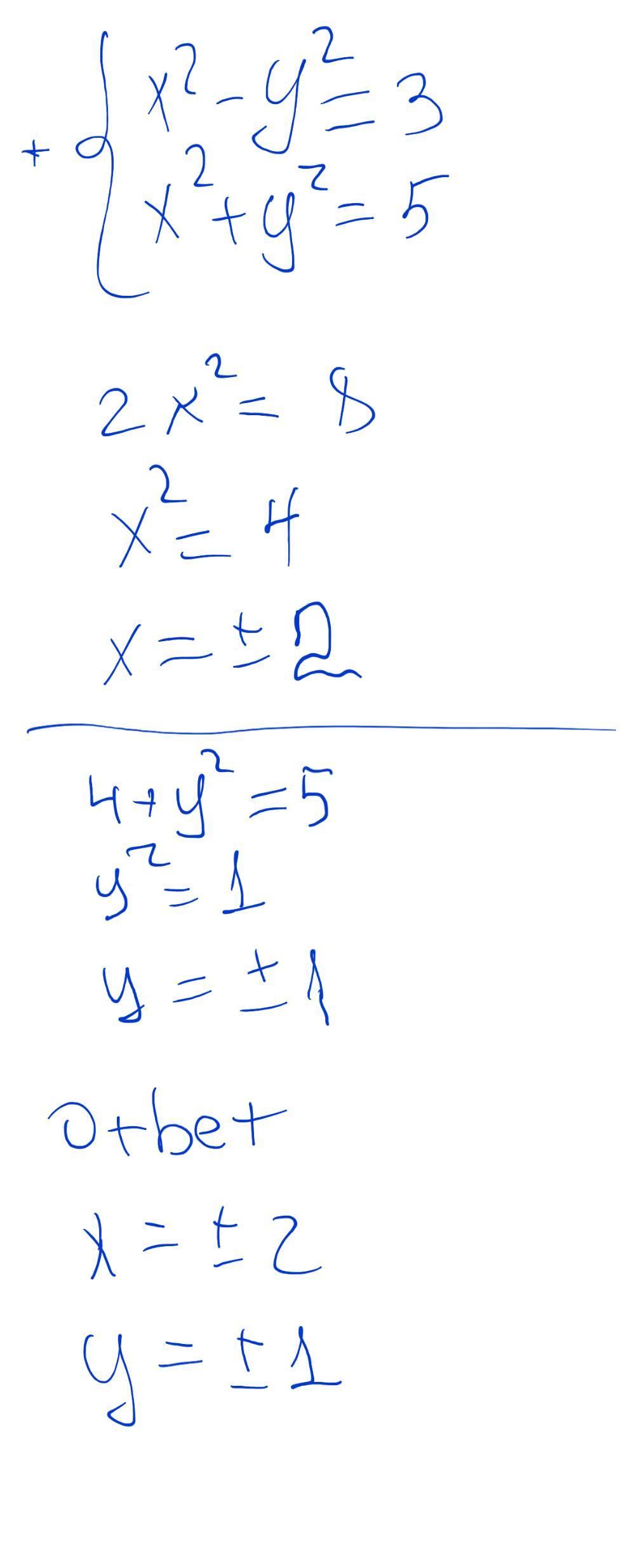
Похожие вопросы
Предмет: Русский язык,
автор: Pangolin555
Предмет: Другие предметы,
автор: Аня1111111111111111
Предмет: Русский язык,
автор: steshinadasha343
Предмет: Информатика,
автор: andreydem90608
Предмет: Математика,
автор: 5t6t