Предмет: Геометрия,
автор: L1mpik
катети прямокутного трикутника відносяться як 1:3 а його площа дорівнює 6см^2. знайти гіпотенузу цього трикутника
Ответы
Автор ответа:
2
Відповідь:
2√10 см.
Пояснення:
Нехай катет а=х см, катет в=3х см, тоді за формулою площі трикутника
1/2 * х * 3х = 6
1,5х²=6; х²=4; х=2
а=2 см; в=2*3=6 см
За теоремою Піфагора с=√(а²+в²)=√(4+36)=√40=2√10 см.
Автор ответа:
3
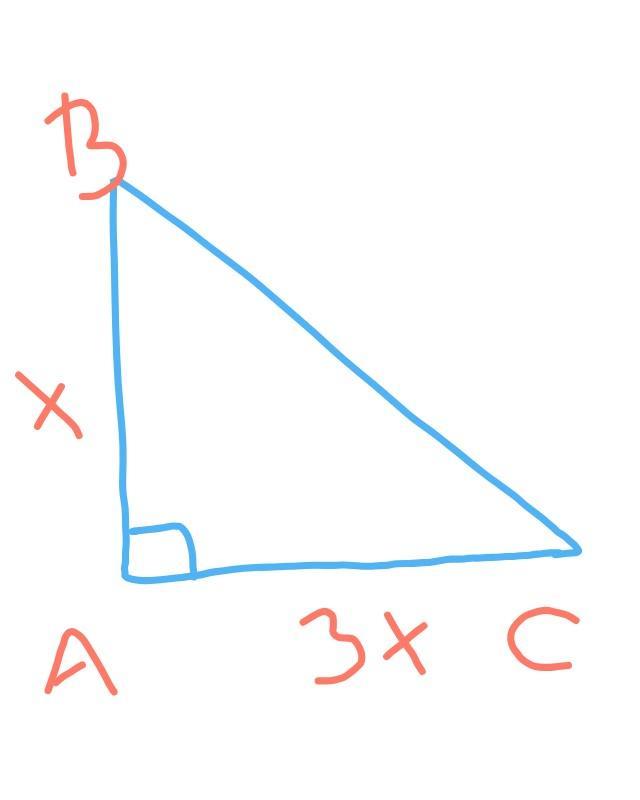
Если АВ:АС = 1:3, то пусть АВ = х, тогда АС = 3х. Площадь прямоугольного треугольника равна половине произведения его катетов.
Тогда
АВ = 2 см, АС = 6 см.
По теореме Пифагора ВС^2 = АВ^2+АС^2 ;
ВС^2 = 40 ; ВС = 2√10.
Ответ : 2√10.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: НастяКароч
Предмет: Русский язык,
автор: vika1402
Предмет: Другие предметы,
автор: tanyabic
Предмет: Математика,
автор: димаш36
Предмет: Алгебра,
автор: EgorPELMEN