Бічна сторона рівнобедреного трикутника дорівнює 25см. Знайдіть основу трикутника якщо його площа 168см кв. 88 балов
Ответы
Відповідь
14 см
Пояснення:
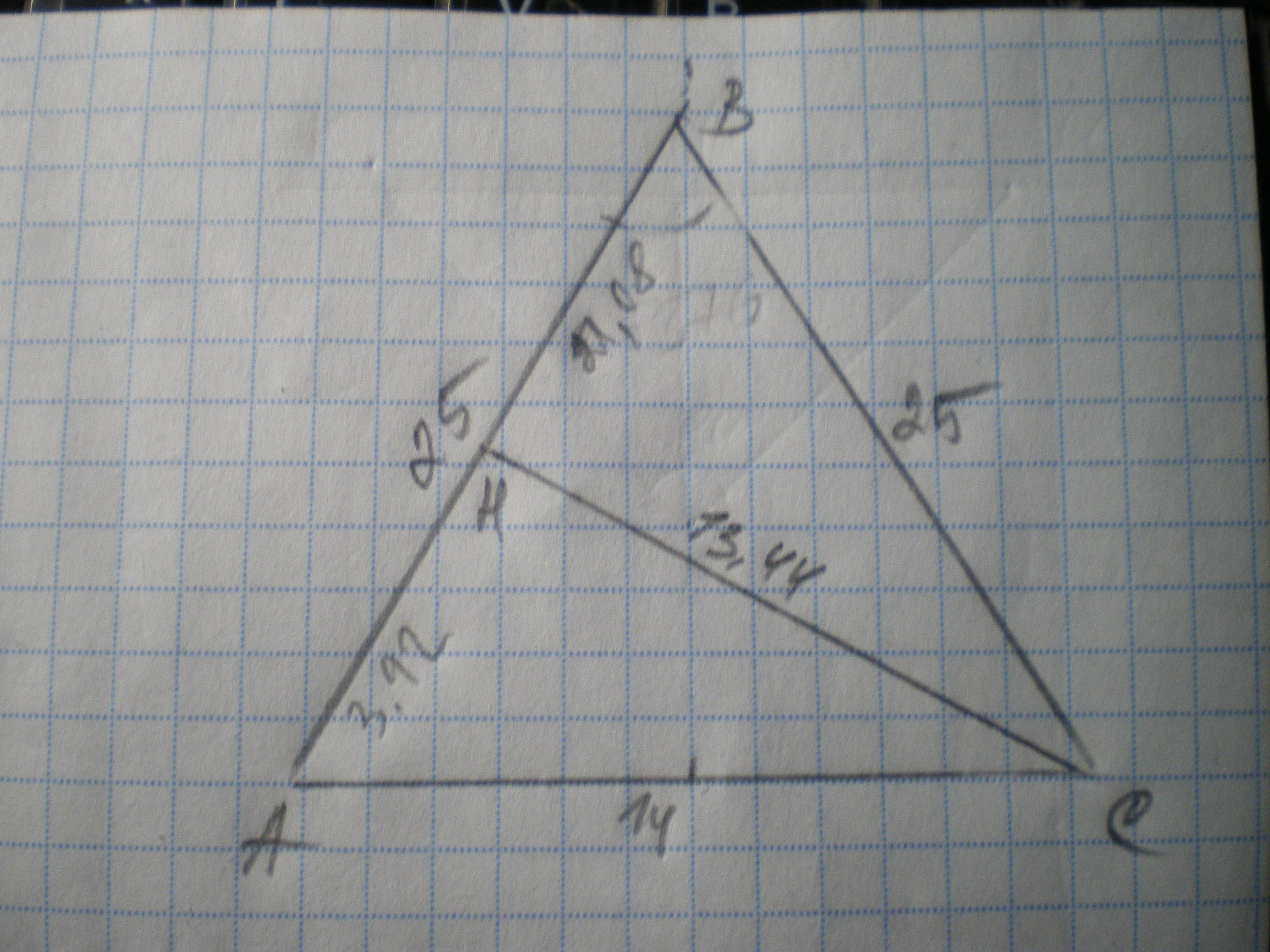
Дано: ΔАВС, АВ=ВС=25 см. S (АВС)=168 см². Знайти АС.
Проведемо висоту СН до бічної сторони, знайдем СН з формули площі трикутника:
168=1/2 * 25 * СН
СН=13,44 см.
За теоремою Піфагора
ВН=√(ВС²-СН²)=√(625-180,6336)=√444,3664=21,08 см
АН=25-21,08=3,92 см.
АС=√(СН²+АН²)=√(180,6336+15,3664)=√196=14 см
Высота, проведенная к основанию, является и медианой,
половина произведения основания на высоту дадут площадь, но эту же площадь можно получить, если умножить боковую сторону на высоту х, проведенную к этой стороне, т.е. 25*х/2=168, откуда х=2*168/25=336/25=13.44
Найдем теперь часть боковой стороны, которая делится высотой, проведенной к бок. стороне, начиная от вершины треугольника.
она равна √(625-180.6336)=√(444.3664)=21.08
значит, оставшаяся часть боковой стороны
25-21.08=3.92
используем ее для нахождения высоты, проведенной к основанию.
из прямоуг. треугольника, образованного частью бок. стороны, и высотой, проведенной к основанию, находим основание.
√(21.08²+3.92²)=√(180.6336+15.3664)=√196=14/см/
Ответ 14 см