Предмет: Математика,
автор: НеизвесныйХ
Решите пожалуйстааааааааааааа
Приложения:
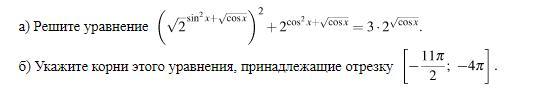
Ответы
Автор ответа:
0
а)
ОДЗ:
, т.к. степень всегда
Замена:
приводим к общему знаменателю
Обратная замена:
, n∈Z
учтем условия одз. значит , n∈Z
б)
Похожие вопросы
Предмет: Русский язык,
автор: larissska
Предмет: Русский язык,
автор: shabnina
Предмет: Английский язык,
автор: 72295
Предмет: Алгебра,
автор: Wwwelina
Предмет: Математика,
автор: 1234567890вавава