Пожалуйста,решите последние два.
Ответы
Ответ:
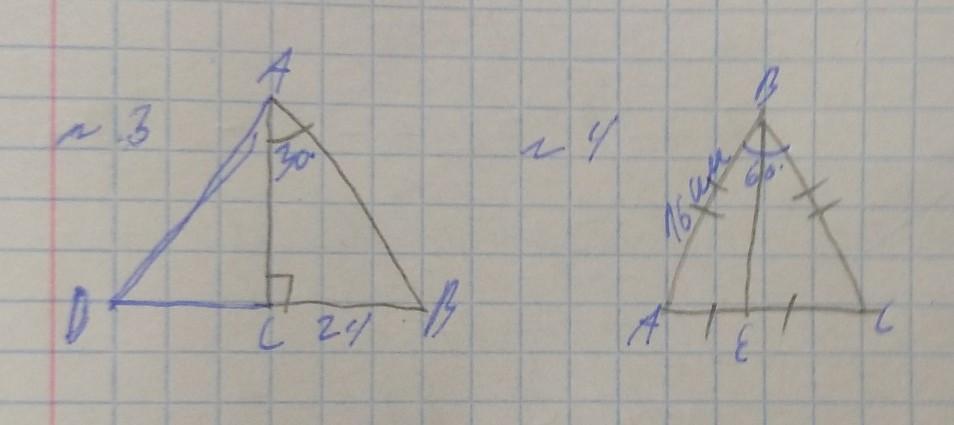
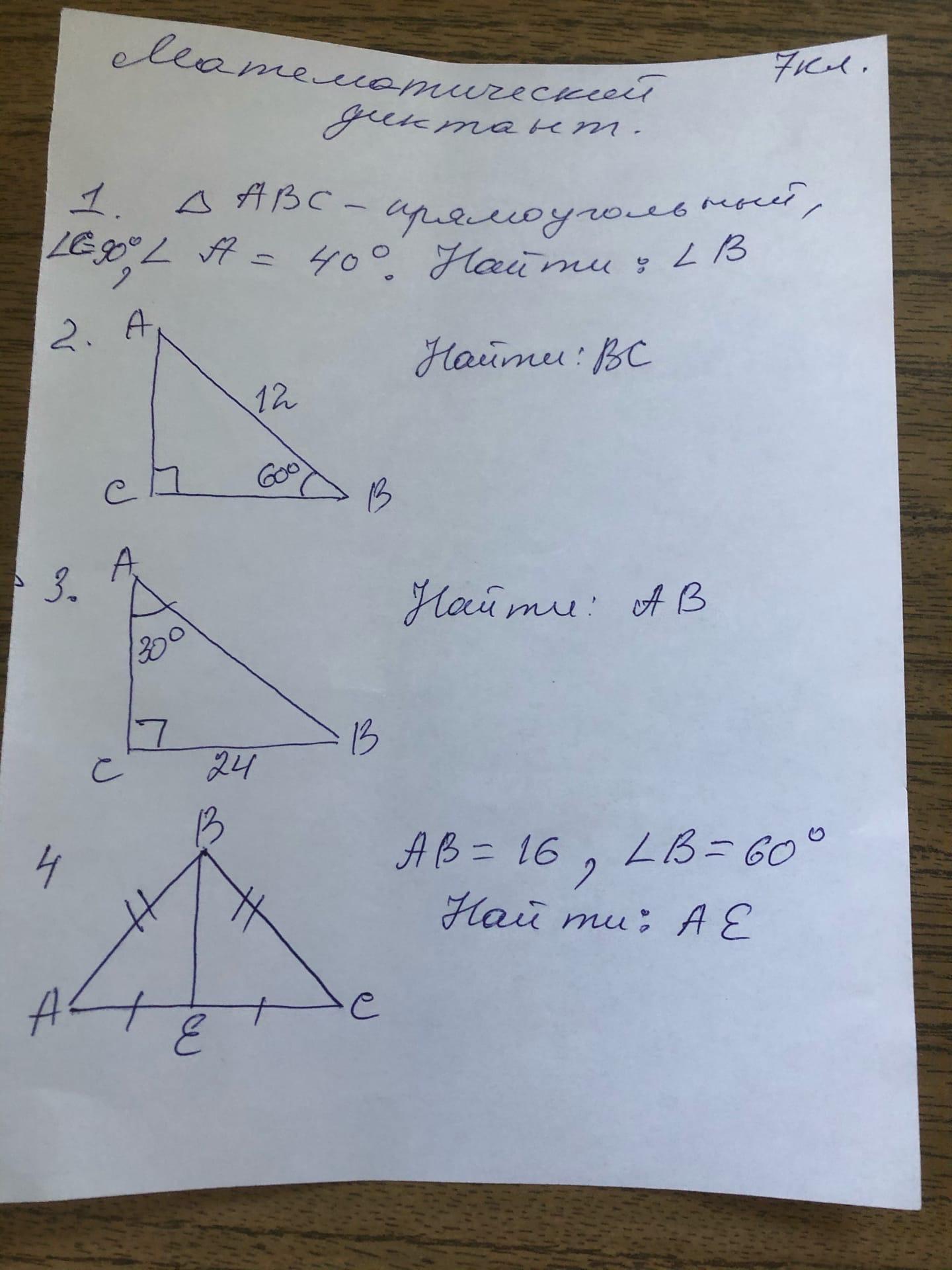
№3
Дано:
(знак треугольника) ABC
(знак угла) BAC=30°
(знак угла) ACB=90°
CB= 24 см
---------
Найти: AB
(рисунок срисовать)
Решение:
1) (знак угла) ABC=180-90-30=60°(По теореме сумма всех углов)
2)сделаем(знак треугольника) ABD=> (знак угла) A=(знак угла)D=60°=>DB=AB=>DB=2CB=>AB=2CB(по свойству прямоуг. треугольника)
3)AB=2•24=48 см
Ответ: AB= 48 см
№4
Дано:
(знак треугольника) ABC
BE=биссектриса
(знак угла) B=60°
AB=16 см
¯¯¯¯¯
Найти: AE
(срисовать рисунок)
Решение:
1)AB=BC, AE=EC, BE- биссектриса => (знак треугольника) ABE=(Знак треугольника) EBC=> BEC и АЕВ=90°, ЕВС и АВЕ=30°
2)(знак угла) ВАЕ=ВСЕ=>АЕ=2ЕВ=ВС=2ЕВ(По свойству прямоуг. треугольника)
3)BC=AB=> EB=16:2= 8 см
Ответ: EB=8 см.
Объяснение:
Свойства прямоугольного треугольника
В прямоугольном треугольнике гипотенуза больше катета.
Катет, лежащий против угла, величина которого равна 30°, равен половине гипотенузе.
Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Теорема о сумме углов треугольника
Сумма углов треугольника равна 180°