Question

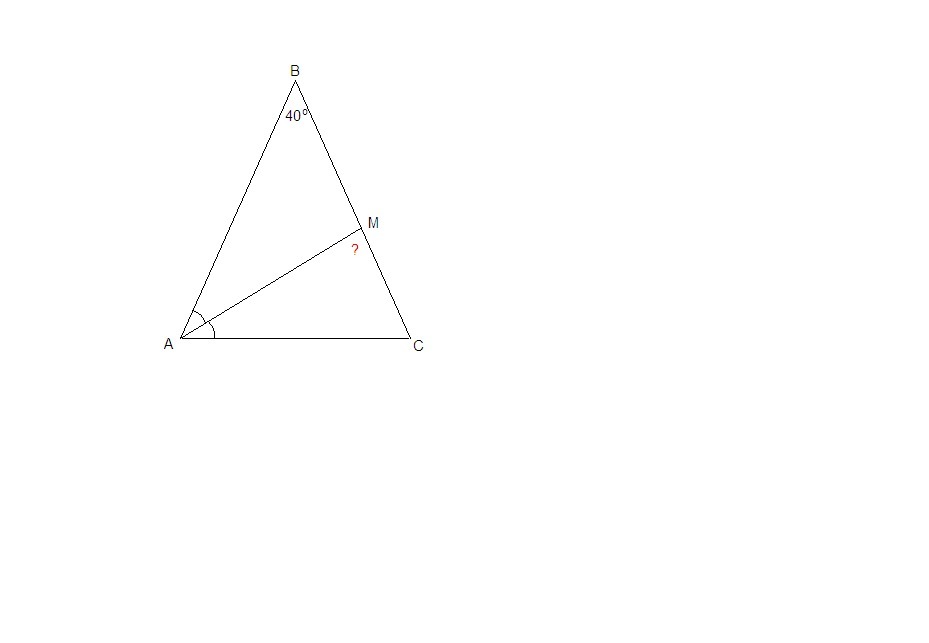
угол при вершине равнобедренного треугольника =40 градусов. Найдите острый угол между биссектрисой угла при основании и противоположной стороной

Answer 1

Углы при основании равнобедренного треугольника равны.
∠ВАС = ∠ВСА = (180° - ∠АВС) /2 = (180° - 40°) /2 = 140° / 2 = 70°.

Биссектриса АМ делит угол ВАС пополам, следовательно
∠МАС = ∠ВАС /2 = 70° / 2 = 35°.

ΔАМС:
∠АМС = 180° - (∠МАС + ∠МСА) = 180° - (35° + 70°) = 180° - 105° = 75°