Предмет: Алгебра,
автор: Was5tn
Можете пожалуйста помочь!!! Алгебра, 85 баллов
Приложения:
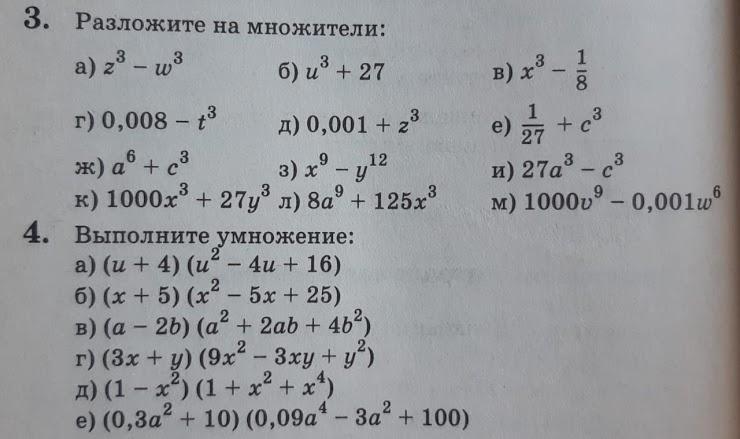
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решение
3.
а) =
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
Приложения:

Was5tn:
Спасибо!
Похожие вопросы
Предмет: Українська мова,
автор: ktyf93
Предмет: Қазақ тiлi,
автор: Рома1арнольд
Предмет: Русский язык,
автор: IrivaVis
Предмет: Математика,
автор: nika1217
Предмет: Математика,
автор: Аноним