Question

Высота правильной четырехугольной пирамиды равна 2 см и составляет с плоскостью боковой грани угол 45°. Найдите плошадь полной поверхности пирамиды.

Answer 1

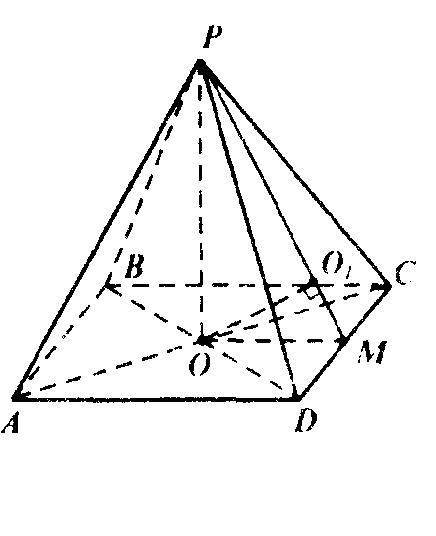
Пусть M — середина ребра CD пирамиды РАBCD. Тогда проекция О1 точки О на плоскость PCD попадает на прямую РМ.

Таким образом ∠ОРМ=45°

Тогда ОМ= $\frac{1}{2}$ AD =  h · tg(45°)

AD= 2h · tg(45°)

PM = $\frac{h}{cos(45)}$

Sполн.пов.= 4$h^{2}$ $tg^{2}$(45°) + 2$\frac{h}{cos(45)}$ · 2h ·tg(45°) = 4$h^{2}$$tg^{2}$(45°)+$4h^{2}$$\frac{sin(45)}{cos(45)}$

Sполн.пов.= 4·4·1+4·4·((√2/2)/(√2/2))= 16+16= 32(см)

Ответ: Sполн.пов.= 32 см