Решите систему уравнений
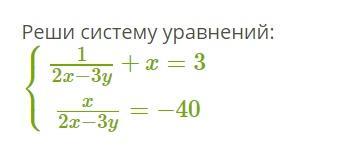
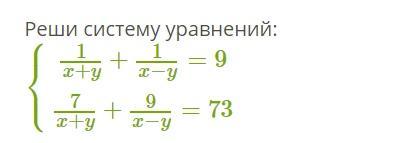
Ответы
Ответ:
1)Решение системы уравнений х₁= -5 х₂=8
у₁= -3,375 у₂=5,4
2)Решение системы уравнений х=9/40
у=1/40
Объяснение:
1)1/(2х-3у)+х=3
х/(2х-3у)= -40
Умножаем оба уравнения на (2х-3у), чтобы избавиться от дроби:
1+х(2х-3у)=3(2х-3у)
х= -40(2х-3у)
Раскрываем скобки:
1+2х²-3ху=6х-9у
х= -80х+120у
Во втором уравнении выразим у через х:
-120у= -80-х
-120у= -81х
у= -81х/-120 сократим дробь на 3:
у=27х/40
Подставим значение у в первое уравнение:
1+2х²-3ху=6х-9у
1+2х²-3х*(27х/40)=6х-9*(27х/40)
1+2х²-81х²/40=6х-243х/40
Умножим уравнение на 40, чтобы избавится от дроби:
40*1+40*2х²-81х²=40*6х-243х
Выполним умножение и перенесём оставшиеся неизвестные в левую часть уравнения:
40+80х²-81х²-240х+243х=0
Приведём подобные члены:
-х²+3х+40=0
х²-3х-40=0, квадратное уравнение, ищем корни:
х₁,₂=(3±√9+160)/2
х₁,₂=(3±√169)/2
х₁,₂=(3±13)/2
х₁= -10/2
х₁= -5
х₂=16/2
х₂=8
Вычислим у:
у=27х/40
у₁=27*(-5)/40
у₁= -135/40
у₁= -3,375
у₂=27*8/40 сокращение на 8
у₂=27/5
у₂=5,4
Решение системы уравнений х₁= -5 х₂=8
у₁= -3,375 у₂=5,4
2)1/(х+у)+1/(х-у)=9
7/(х+у)+9/(х-у)=73
Общий знаменатель (х-у)(х+у), надписываем над дробями дополнительные множители, избавляемся от дроби:
(х-у)+(х+у)=9(х-у)(х+у)
7(х-у)+9(х+у)=73(х-у)(х+у)
Умножим первое уравнение на -7, сложим уравнения по методу алгебраического сложения и выразим х через у.
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
-7(х-у)-7(х+у)= -63(х-у)(х+у)
7(х-у)+9(х+у)=73(х-у)(х+у)
Складываем уравнения:
-7(х-у)+7(х-у)-7(х+у)+9(х+у)=-63(х-у)(х+у)+73(х-у)(х+у)
Приводим подобные члены:
2(х+у)=10(х-у)(х+у) сократим на 2(х+у):
1=5(х-у)
1=5х-5у
-5х= -5у-1
5х=5у+1
х=5у+1/5
Получили выражение х через у. Подставим выражение в первое уравнение и вычислим у:
(х-у)+(х+у)=9(х-у)(х+у)
х-у+х+у=9(х-у)(х+у)
2х=9(х-у)(х+у), или по формуле разности квадратов:
2х=9(х²-у²)
2х=9х²-9у²
2*(5у+1/5)=9(5у+1/5)²-9у²
[2(5у+1)]/5=[9(25у²+10y+1)]/25-9у²
(10у+2)/5=(225у²+90у+9)/25-9у²
Умножим уравнение на 25, чтобы избавиться от дроби:
5(10у+2)=225у²+90у+9-25*9у²
Перенесём неизвестные в левую часть, известные в правую)
50у-225у²-90у+225у²=9-10
Приводим подобные члены:
-40у= -1
у= -1/-40
у=1/40
Вычисляем х:
х=5у+1/5
х=(5*1/40)/5
х=(9/8)/5=9/40
х=9/40
Решение системы уравнений х=9/40
у=1/40