Предмет: Алгебра,
автор: SilverGravity
Решить неравенство.......
Приложения:
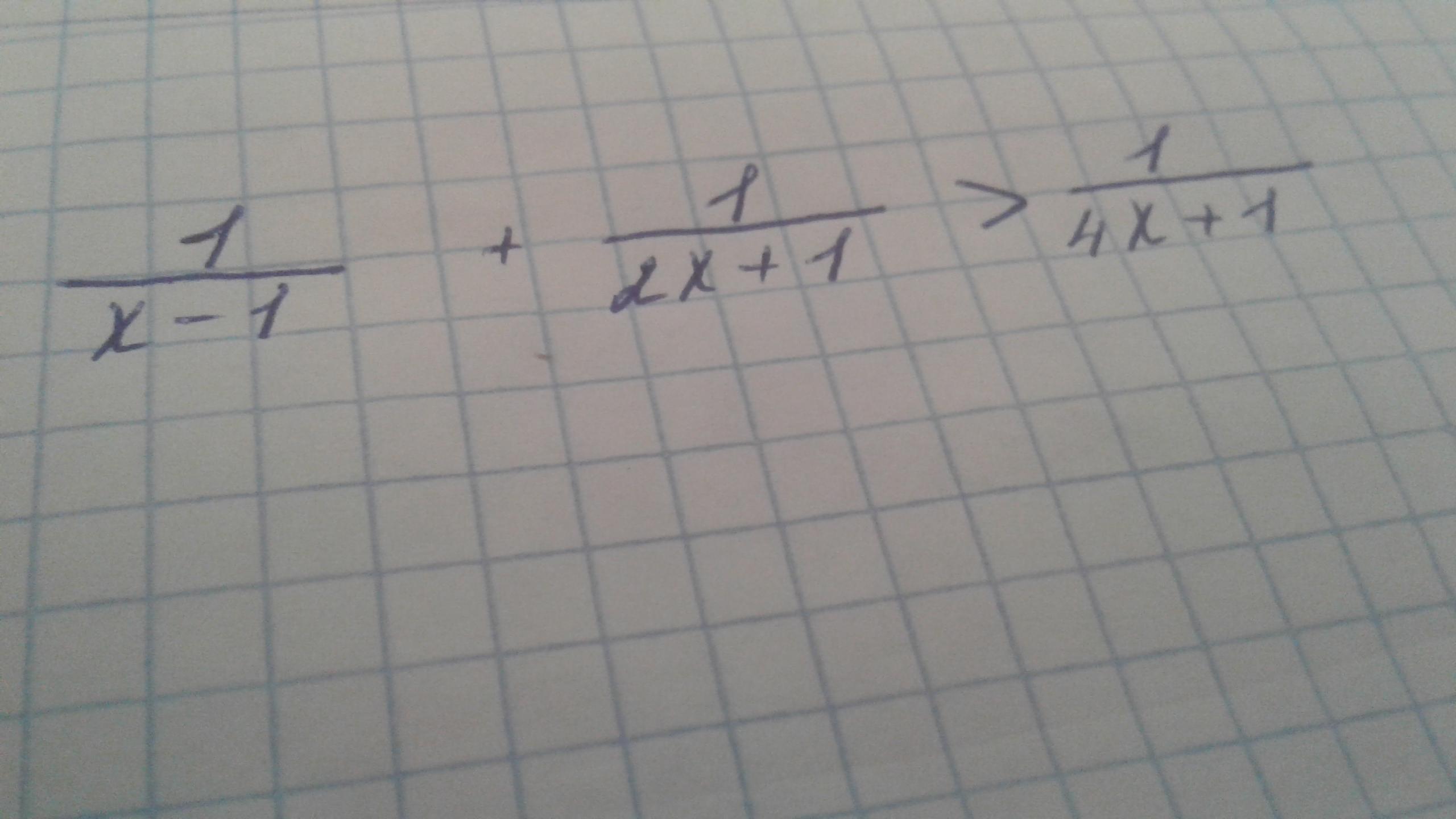
Ответы
Автор ответа:
1
SilverGravity:
Спасибо большое, сможете ещё один решить?
Всё измеНила
Похожие вопросы
Предмет: Русский язык,
автор: dimduganow2012
Предмет: Русский язык,
автор: анюкакри
Предмет: Английский язык,
автор: 4yMavoi
Предмет: География,
автор: bzulaev
Предмет: Математика,
автор: dimadebolsky