Предмет: Геометрия,
автор: euphoria9
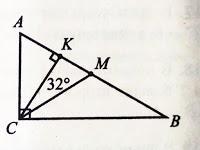
Дан прямоугольный треугольник ABC. ∠С=90º. CK-высота. CM- медиана. ∠KCM=32º. Найдите ∠CMB, ∠MCB, ∠KAC, ∠ACK.
Приложения:
Ответы
Автор ответа:
3
Ответ:
∠СМВ = 122º
∠МСВ = 29º
∠КАС = 61º
∠АСК = 29º
Объяснение:
Так как ∠АКС = 90º, то ∠СКМ = 90º. ==> ∠КСМ + ∠КМС = 90º. ==> ∠КМС = 90º - 32º = 58º.
Так как ∠КМС + ∠СМВ = 180 как смежные ==> ∠СМВ = 180º - 58º = 122º.
Медиана в прямоугольном треугольнике, проведённая из прямого угла к гипотенузе, будет равна половине гипотенузы. ==> СМ = МВ ==> МСВ - равнобедренный ==> углы при основании равны ==> ∠МСВ = (180º - 122º) : 2 = 58º : 2 = 29º
∠АСК = ∠АСВ - ∠КСМ -∠МСВ = 90º - 32º - 29º = 58º - 29º = 29º.
∠КАС = 90º - 29º = 61º.
Попрошу вас перепроверить мой ответ, чтобы сходилось всё, а так должно быть правильно
Похожие вопросы
Предмет: Русский язык,
автор: gtxtymrj
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: smolovik2008
Предмет: Геометрия,
автор: Novikova640
Предмет: Математика,
автор: katyaporfiryeva