Предмет: Математика,
автор: SemLemik
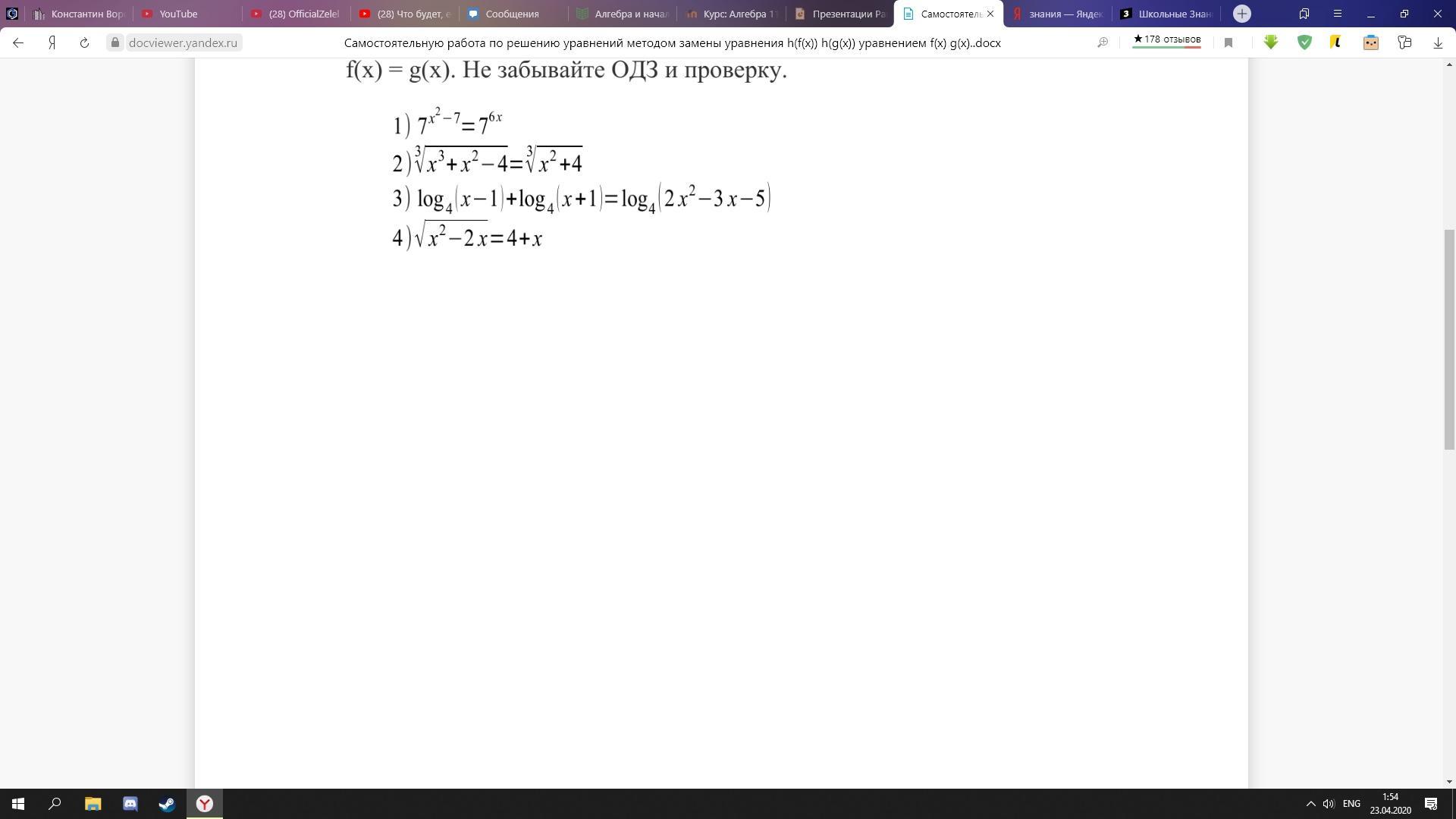
Помогите решить!! Метод разложения на множители
Приложения:
Ответы
Автор ответа:
0
SemLemik:
Спасибо конечно, но нужно решить другим способом: методом разложения на множители
Этот способ я и так знаю)
Похожие вопросы
Предмет: Українська мова,
автор: konter
Предмет: Русский язык,
автор: 15287
Предмет: Русский язык,
автор: телефончики
Предмет: Химия,
автор: ZloiPodrostok1
Предмет: Алгебра,
автор: SeeTheSea