Предмет: Геометрия,
автор: Аноним
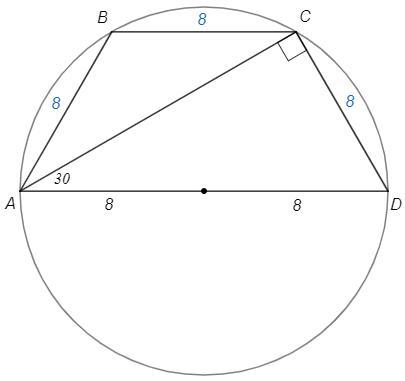
помогите решить подробно с чертежом Найти периметр равнобедренной трапеции, диагональ которой
перпендикулярна боковой стороне и образует с основанием угол 30 градусов, если радиус окружности, описанной около трапеции, равен 8 см.
Аноним:
пожалуйста очень нужно сейчас это решение
через 10 мин
Ответы
Автор ответа:
6
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: denisenkoma
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: ПОЛЬЗОВАТЕЛЬ20161