Предмет: Математика,
автор: phormaline93
нужно найти производную сложной функции! Три задания
Приложения:
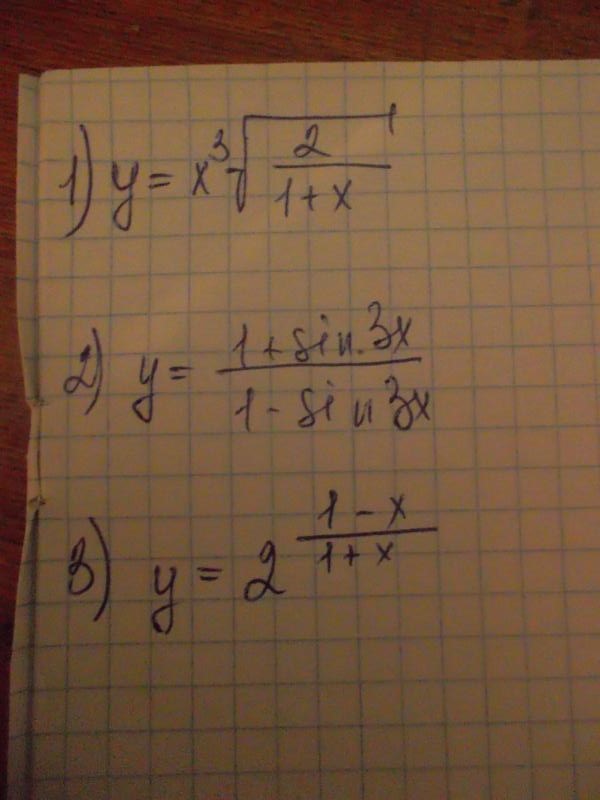
Ответы
Автор ответа:
0
решение добавил........................
X^3*sqrt(2/1+x)
F'(x)=3x^2sqrt(2/1+x)-x^3*1/2*sqrt(x+1)/sqrt(2)*2*1/(x+1)^2=
=x^2*sqrt(2/1+x)(3-x/2*(x+1))=((5x+6)*x^2/(x+1))*sqrt(1/2(1+x))
X^3*sqrt(2/1+x)
F'(x)=3x^2sqrt(2/1+x)-x^3*1/2*sqrt(x+1)/sqrt(2)*2*1/(x+1)^2=
=x^2*sqrt(2/1+x)(3-x/2*(x+1))=((5x+6)*x^2/(x+1))*sqrt(1/2(1+x))
Приложения:

Похожие вопросы
Предмет: Биология,
автор: any1236
Предмет: Физика,
автор: 6308497
Предмет: История,
автор: Ulyana20081229
Предмет: Математика,
автор: Алипия
Предмет: Алгебра,
автор: loooolD