Question

Постройте график функции $\boldsymbol{f(x)=\dfrac{x-2{x}^{2}}{x-2}}$.

(достаточно будет найти асимптоту, пересечения с осями, ну и соответственно привести саму таблицу с точками)

Answer 1

Ответ:

1) - "Инструкция по построению графика своими руками";

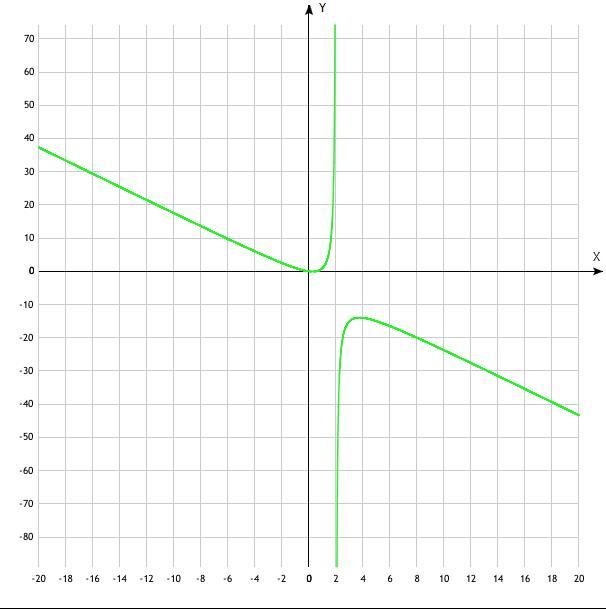
2) - Сам график;

3). - Асимптоты.

_____________________________________

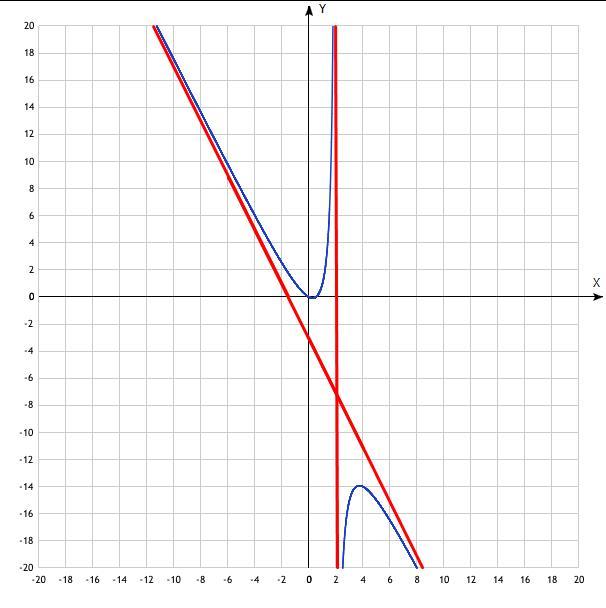
Асимптоты здесь - это вертикальная прямая, параллельная оси ординат и проходящая через точку $\emph {(2;0)}$ (задается уравнением $\emph {x = 2}$) и наклонная, которая, как показывают вычисления, является графиком линейной функции $\emph {y = - 2x - 3}$.

Пересечения с осями координат происходят в точках $\emph {(0;0)}$ и $\emph {(0,5;0)}$. Чтобы их найти, достаточно в уравнение, задающее функцию, поочередно подставить $\emph {x = 0}$ и $\emph {y = 0}$.

А таблица точек - в прикрепленном файле.