Предмет: Математика,
автор: Аноним
Геометрия. Помогите пж кто сможет
Приложения:
nikebod313:
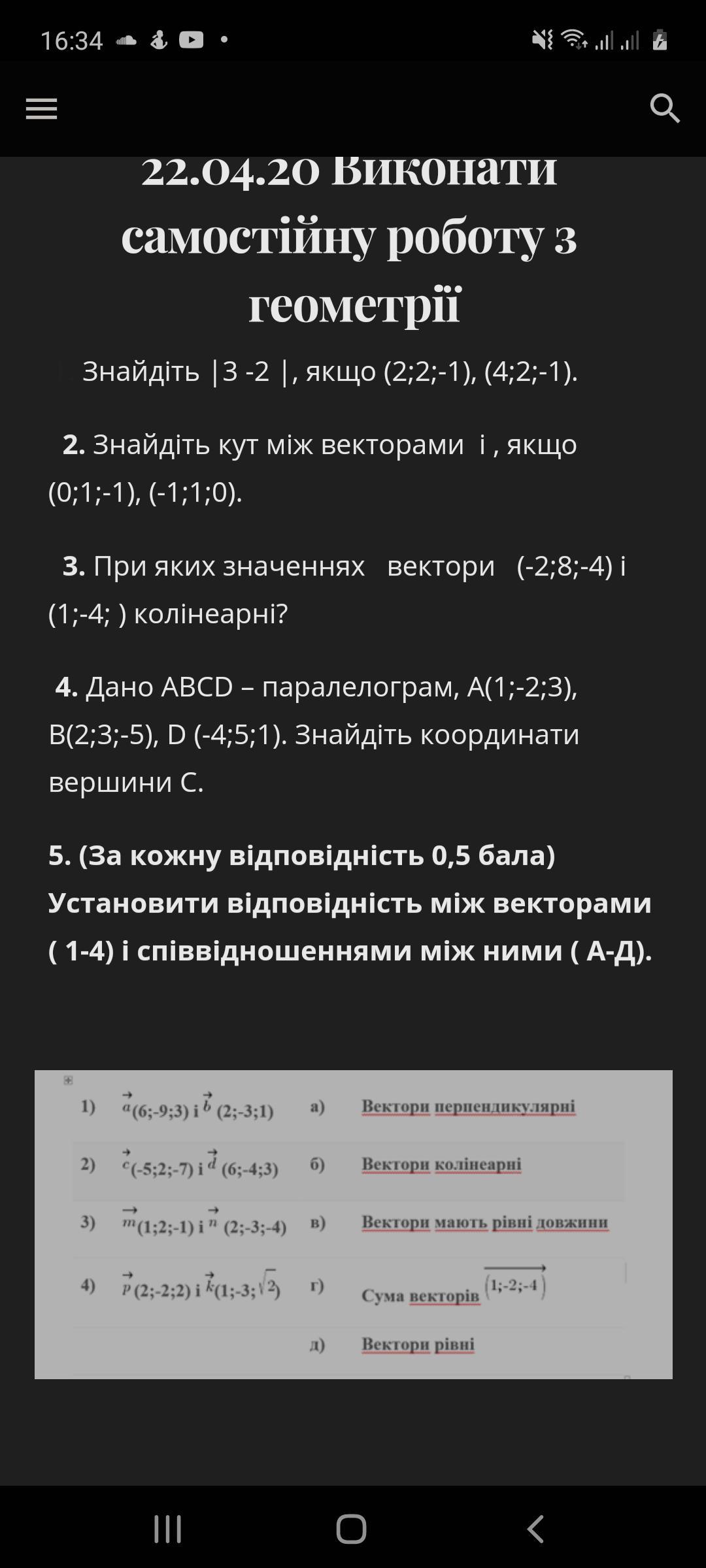
В третьем задании не дописана последняя координата вектора (1; -4; ?)
Ответы
Автор ответа:
1
Відповідь:
Скалярний добуток двох векторів:
Довжини векторів:
Наслідок зі скалярного добутку двох векторів:
, де
Отже,
Відповідь:
Умова колінеарності векторів:
Отже,
Відповідь:
Тут
Тоді , отже,
Нехай . Тоді
Ставимо у відповідність координати вектора :
Відповідь:
Відповідь: 1—б; 2—г; 3—а; 4—в.
Похожие вопросы
Предмет: Русский язык,
автор: alle326
Предмет: Русский язык,
автор: 240601
Предмет: Другие предметы,
автор: sarkisian2002
Предмет: Литература,
автор: Стася20171
Предмет: Математика,
автор: Artur2018