Question

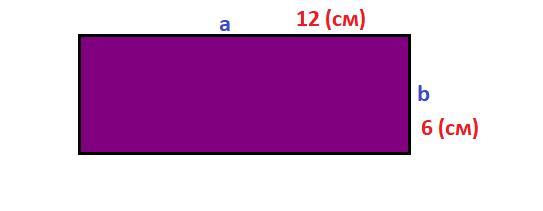
Одна из сторон прямоугольника на 6 см меньше другой. Найдите стороны прямоугольника, если его площадь равна 72 см2.

Answer 1

Решение:

Пусть $x$ (см) равна длина прямоугольника, тогда ширина равна $(x-6)$ (см). Площадь данного прямоугольника равна $72$ (см²). Составим и решим квадратное уравнение.

$\boldsymbol{S=a\cdot b} \Longrightarrow \\\\x\cdot (x-6)=72\\\\x^2-6x-72=0\\\\x^2+6x-12x-72=0\\\\x\cdot\underline{(x+6)}-12\cdot\underline{(x+6)}=0\\\\(x+6)(x-12)=0\\\\\left \{ {{x+6=0} \atop {x-12=0}} \right. \Rightarrow \left \{ {{x_1=-6} \atop {x_2=12}} \right.$

Итак, уравнение имеет два корня (можно проверить по дискриминанту). Поскольку длина не может быть отрицательным числом, то 1 корень нам не подходит. Т.е. длина равна $\underline{12}$ (см).

Поэтому исходя из этого, ширина равна $12-6=\underline{6}$ (см).

Проверка. $\boldsymbol{S=ab=12\cdot6=72}$ (см²) ⇒ решено верно!

Ответ:  $\Large { \boxed { \bold { a=12}} }$ (см);  $\Large { \boxed { \bold { b=6}} }$ (см).