Question

Помогите с геометрией 8 класс пожалуйста!

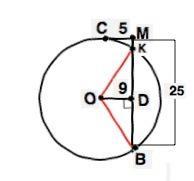
Дана окружность (О; ОС). Из точки М, которая находится вне окружности, проведена секущая МВ и касательная МС.
ОD - перпендикуляр, проведённый из центра окружности к секущей МВ и равный 5 см.
Найдите радиус окружности, если известно, что МВ=25 см и МС=5 см.

Заранее спасибо!

Answer 1

Обозначим вторую точку пересечения секущей с окружностью – К. 

Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной. 

СМ²=МВ•MK

25=25•MK ⇒ МК=1

ВК=25-1=24 см

 ОК=ОВ – радиусы к точкам пересечения секущей и окружности. 

∆ КОВ - равнобедренный, OD⊥KB ⇒OD - медиана и высота. 

КD=24:2=12 

Из ∆ OKD  по т.Пифагора

OK²=KD²+OD² ⇒OK=√(144+81)

OK=R=√225=15 см