Предмет: Алгебра,
автор: dasatotackaa
ПОМОГИТЕ!!!
Точка движется прямолинейно по закону S ( t ) =( 1/ 4* t ^4) - 2 *^t 3 + (9/2*t^2) + 2 , где S измеряется в метрах, t - в секундах. В какой наибольший момент времени ускорение движения равна 0 ?
Приложения:
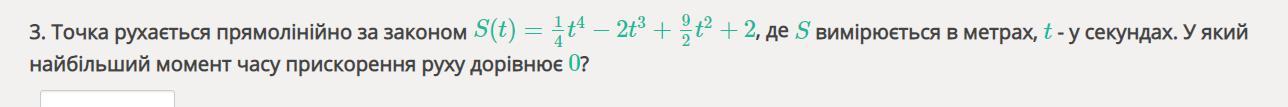
Ответы
Автор ответа:
1
Воспользуемся физическим смыслом производной: ускорение есть производная от скорости:
В свою очередь - в случае прямолинейного движения - скорость есть производная от перемещения, т.е. .
Находим закон скорости:
Находим закон ускорения:
По условию ,
По теореме Виета
, откуда
.
Искомый момент времени - .
ОТВЕТ: t = 3.
Похожие вопросы
Предмет: Русский язык,
автор: BeLyAeVa24
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: алиника
Предмет: Физика,
автор: SadBoys111
Предмет: География,
автор: Лезефина45555