СРОЧНО
Два угла треугольника равны 40 градусов И 52 градуса. Найдите тупой угол который образуют высоты треугольника выходящие из вершин этих углов
Ответы
Два угла треугольника равны 40° и 52°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов.
- - -
Дано :
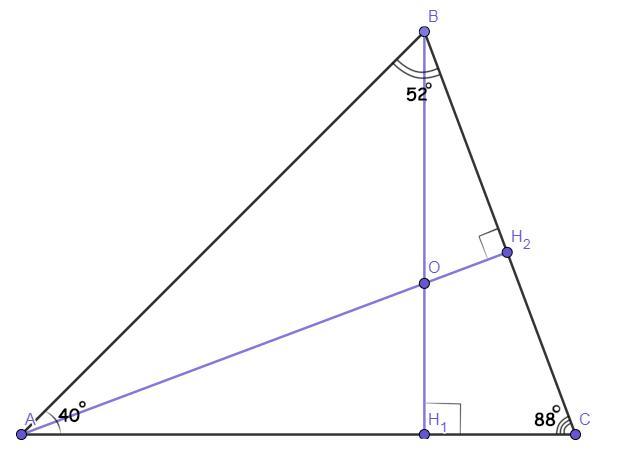
ΔАВС.
∠А = 40°.
∠В = 52°.
ВН₁ и АН₂ - высоты.
Точка О - ортоцентр (точка пересечения высот).
Найти :
∠АОВ = ? (или ∠Н₁ОН₂, не важно, так как они равны как вертикальные).
Решение :
Немного о расположении ортоцентра О :
Для начала найдём ∠С.
По теореме о сумме углов треугольника -
∠А + ∠В + ∠С = 180°
∠С = 180° - ∠А - ∠В
∠С = 180° - 40° - 52°
∠С = 88°.
Так как все углы ΔАВС - острые, то ортоцентр О лежит внутри ΔАВС.
- - -
Рассмотрим ΔСВН₁ - прямоугольный (так как ∠ВН₁С = 90° по определению высоты треугольника).
- Сумма острых углов прямоугольного треугольника равна 90°.
Тогда -
∠Н₁СВ + ∠Н₁ВС = 90°
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - 88°
∠Н₁ВС = 2°.
Теперь рассмотрим ΔОВН₂ - прямоугольный (так как ∠ОН₂В = 90°).
По выше сказанному -
∠ВОН₂ + ∠ОВН₂ = 90°
∠ВОН₂ = 90° - ∠ОВН₂
∠ВОН₂ = 90° - 2°
∠ВОН₂ = 88°.
- - -
∠ВОН₂ и ∠АОВ - смежные.
- Сумма смежных углов равна 180°.
Следовательно -
∠ВОН₂ + ∠АОВ = 180°
∠АОВ = 180° - ∠ВОН₂
∠АОВ = 180° - 88°
∠АОВ = 92°.
Ответ :
92°.