Предмет: Геометрия,
автор: 72937
Помогите пожалуйста!!!
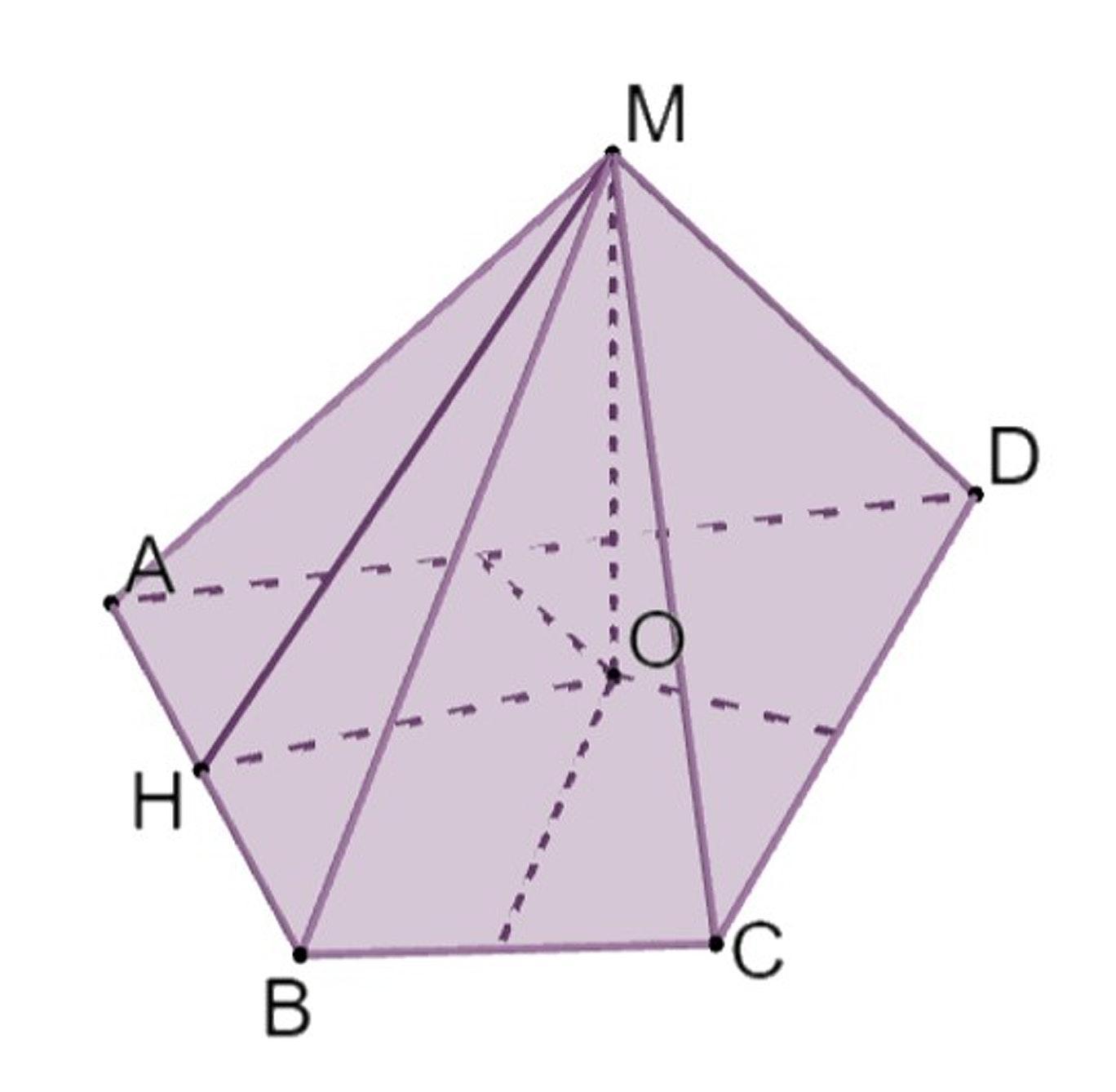
Все двугранные углы при основании четырехугольной пирамиды равны между собой. Высота пирамиды равна 12 м, а периметр и площадь основания равны 48 м и 120 м^2. Найдите площадь боковой поверхности пирамиды
Приложения:
Ответы
Автор ответа:
23
Ответ:
312
Объяснение:
Sб = 1/2 * P * h,
P - периметр основания,
h - высота боковой стороны
Все двугранные углы равны, следовательно высота проходит через центр вписанной окружности.
По формуле радиус вписанной в четырёхугольник окружности
r = 2*S / P,
P - периметр основания,
S - площадь основания
r = 2*120/48 = 5
По т. Пифагора: HM =
HO = r
HM =
HM = 13
Sб = 1/2 * 48 * 13 = 312
Похожие вопросы
Предмет: Английский язык,
автор: moiseevanasten
Предмет: Русский язык,
автор: Гаааав
Предмет: Другие предметы,
автор: levinakaterina
Предмет: История,
автор: sofiaushatova
Предмет: Химия,
автор: gigelxena