Предмет: Геометрия,
автор: 00MaRs00
В прямоугольный треугольник вписана окружность. Точка касания, лежащая на гипотенузе, делит её на отрезки, равные 4 и 6 см.
Найдите площадь данного треугольника.
Ответы
Автор ответа:
6
Ответ:
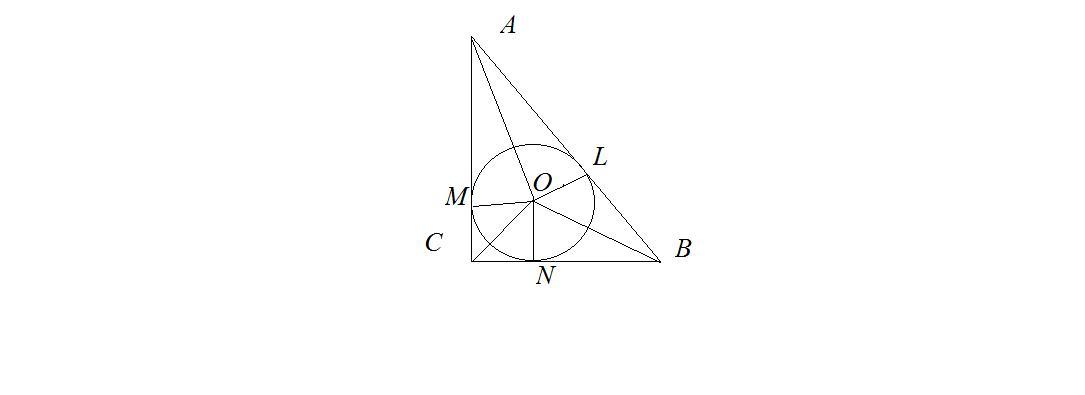
Пусть дан △АВС - прямоугольный ,в него вписана окружность с центром в т.О . BL = 6 см, LA = 4 см.
Найдём S△АВС-?
BN=BL , AL=AM как отрезки касательных , проведённых из одной точки.
СMON-квадрат.По теореме Пифагора :
(6+r)² + (4+r)² , но r -?
36+12r+r²+16+8r+r²=100
2r²+20r-48=0
r²+10r-24=0
r1=-10+14/2=2
r2=-10-14/2=-12(не подходит)
1 катет : LA+r = 4+2=6 см
2 катет : BL+r = 6+2=8 см
S△АВС=1/2*6*8=24 см²
Приложения:
00MaRs00:
Пасбо)
просто самый умный обажаю занаия геметрия за крантин с 3 на 4 перекатилась прсто поцелуйчики обажаю карантин
=))))))))))))))))))))))))))))))))))))))))))))))))
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: charger90
Предмет: Русский язык,
автор: Интиллект48
Предмет: Алгебра,
автор: Reginaa11