Question

 треугольнике два угла равны 64° и 66°. Из этих углов проведены высоты. Найдите угол между этими высотами. Ответ дайте в градусах. 
Варианты ответов:

110°

60°

130°

90°

​

Answer 1

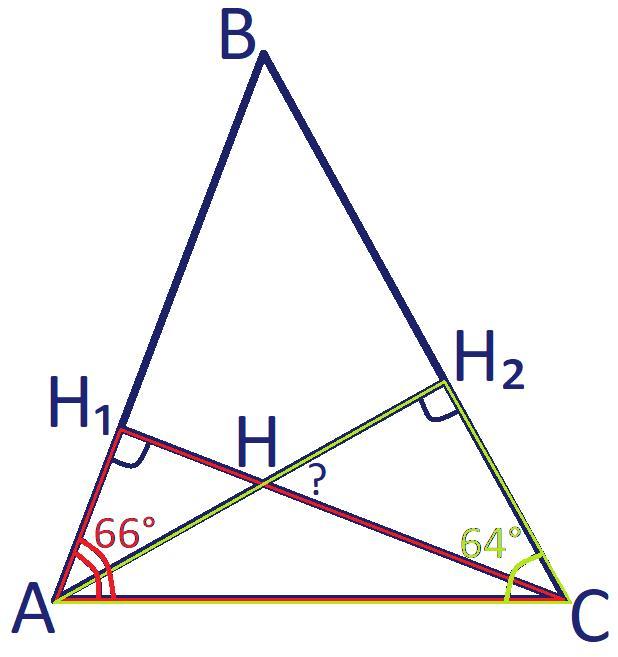
Пусть дан △ABС, при этом ∠A = 66°, ∠С = 64°. CH₁ и AH₂ - высоты между которым нужно найти угол. CH₁ ∩ AH₂ = H.

• Угол между пересекающимися отрезками определяется так же, как и угол между пересекающимися прямыми. Т.е. это один из 4 углов, образованных при пересечении, который не больше 3 других.

△AH₁C - прямоугольный т.к. ∠AH₁C = 90°,

• Сумма острых углов прямоугольного треугольника равна 90°.

∠H₁AC+∠H₁CA = 90°;

∠H₁CA = 90°-∠H₁AC;

∠H₁CA = 90°-66° = 24°.

△CH₂A - прямоугольный т.к. ∠CH₂A = 90°,

По свойству острых углов прямоугольного треугольника:

∠H₂AC+∠H₂CA = 90°;

∠H₂AC = 90°-∠H₂CA;

∠H₂AC = 90°-64° = 26°.

Рассмотрим △AHC:

∠HCA = 24°;  ∠HAC = 26°;

• Сумма внутренних углов треугольника равна 180°.

∠AHC+∠HCA+∠HAC = 180°;

∠AHC = 180°-(∠HCA+∠HAC);

∠AHC = 180°-(24°+26°);

∠AHC = 180°-50° = 130°.

• Сумма смежных углов составляет 180°

∠H₂HC и ∠AHC - смежные,

⇒ ∠H₂HC+∠AHC = 180°;

∠H₂HC = 180°-∠AHC;

∠H₂HC = 180°-130° = 50°.

Вертикальные углы равны, ∠H₂HC < ∠AHC  ⇒  искомый угол составляет 50°.

Ответ: 50.