Предмет: Геометрия,
автор: kyn81
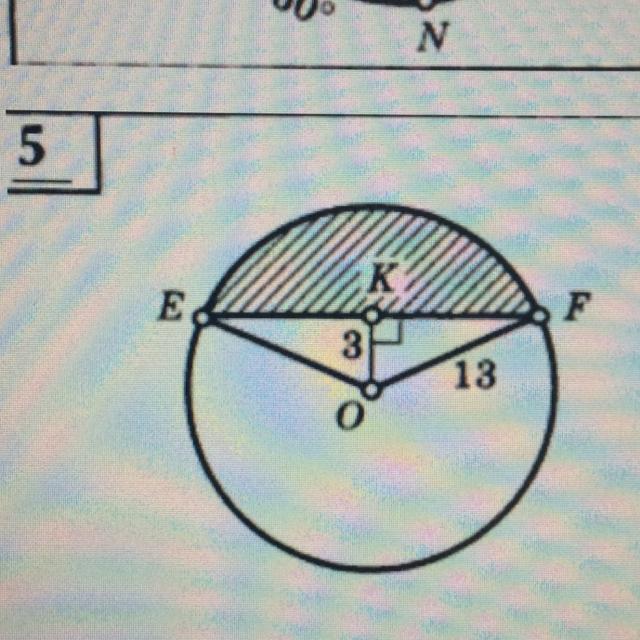
Найдите площадь закрашенной фигуры
Приложения:
Ответы
Автор ответа:
1
1.
Найдём угол EOF
∠EOF = 2*∠KOF
cos (∠KOF) = KO/FO = 3/13
∠KOF = arccos(3/13)
∠EOF = 2*arccos(3/13)
2.
Площaдь треугольника EOF
По т. Пифагора катет KF
KF = √(OF² - OK²) = √(13² - 3²) = √(169 - 9) = √160 = 4√10
EF = 2*KF = 8√10
S(ΔEOF) = 1/2*EF*OK = 1/2*8√10*3 =12√10
3.
Площадь кругового сектора EOF(вычисления в радианах!)
S(∪EOF) = OF²*∠EOF/2 = 13²/2*2*arccos(3/13) = 169*arccos(3/13)
4.
Площадь заштрихованной фигуры
S = S(∪EOF) - S(ΔEOF) = 169*arccos(3/13) - 12√10 ≈ 188.16
Похожие вопросы
Предмет: Русский язык,
автор: sepsate123456sssss
Предмет: Русский язык,
автор: buch30ik
Предмет: Другие предметы,
автор: AdrianoNogueira
Предмет: Математика,
автор: Аноним