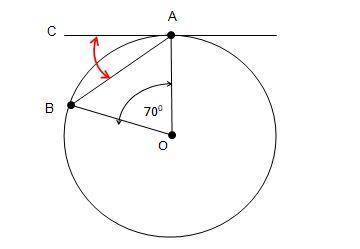
Через конец А хорды АВ окружности с центром О проведена касательная АС. Найти угол
ВАС, если угол АОВ=70 градусов.
Ответы
Ответ:
Объяснение:
Так как ОА = ОВ как радиусы окружности, то треугольник АВР равнобедренный.
Тогда угол ВАО = ВАО = (180 – АОВ) / 2 = (180 – 70) / 2 = 110 / 2 = 550.
По свойству касательной, проведенной к окружности, радиус, проведенный к касательной из центра окружности, перпендикулярен касательной. Тогда угол САО = 900.
Угол ВАС = САВ – ВАО = 90° – 55° = 35°.
Ответ: Угол ВАС равен 35°
Ответ:
Так как ОА = ОВ как радиусы окружности, то треугольник АВР равнобедренный.
Тогда угол ВАО = ВАО = (180 – АОВ) / 2 = (180 – 70) / 2 = 110 / 2 = 550.По свойству касательной, проведенной к окружности, радиус, проведенный к касательной из центра окружности, перпендикулярен касательной. Тогда угол САО = 900.Угол ВАС = САВ – ВАО = 90° – 55° = 35°.
Ответ: Угол ВАС равен 35°
Объяснение: