Question

Выберите правильный ответ.

В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AMB = 30°. Найдите расстояние от точки M до стороны AB. Ответ дайте в сантиметрах.

7 см


24 см


6 см


14 см

Answer 1

Ответ:

7 см

Правильное условие:

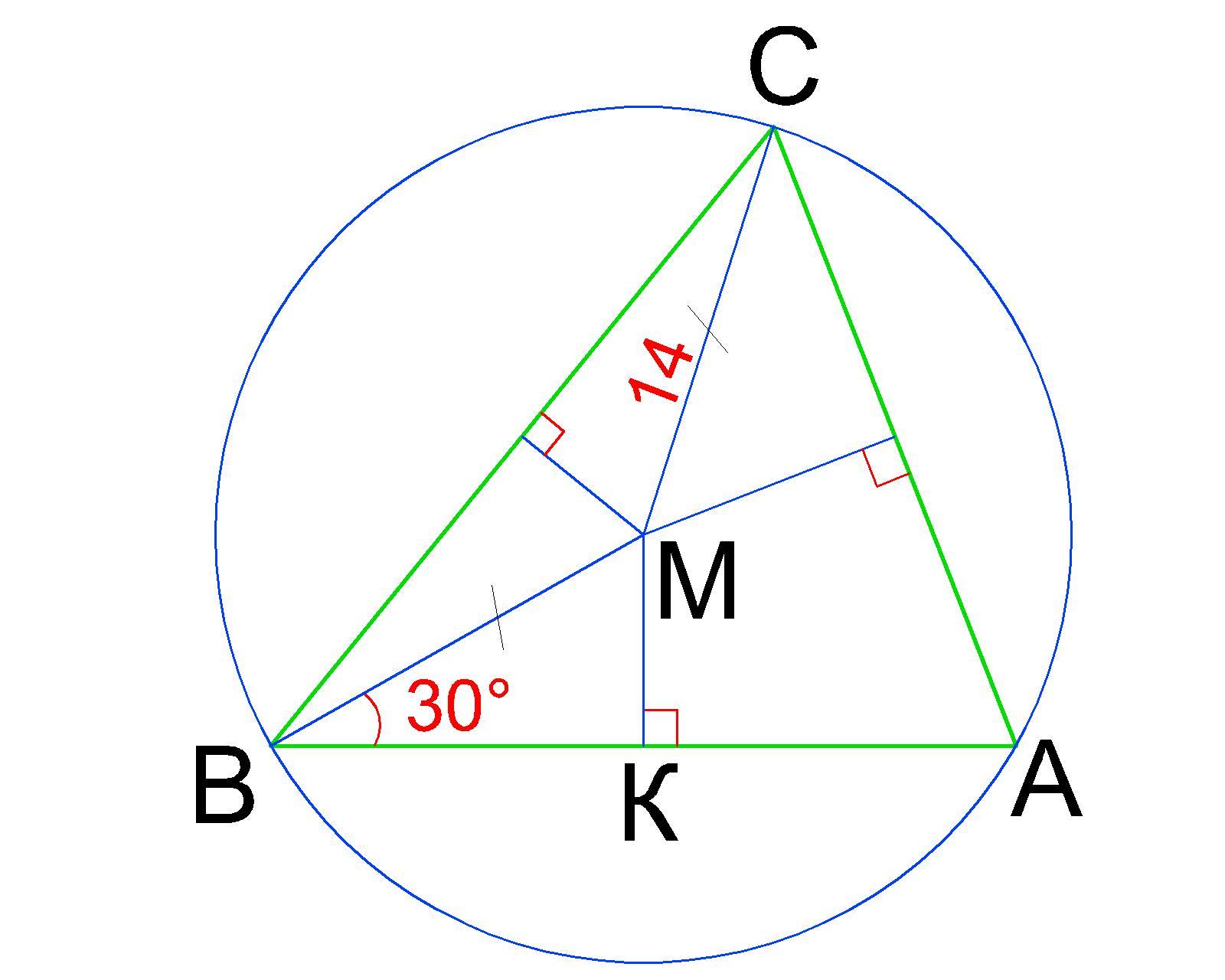
В остроугольном треугольнике ABC серединные перпендикуляры к сторонам BC и AC пересекаются в точке M. Известно, что MC = 14 см, ∠AВМ = 30°. Найдите расстояние от точки M до стороны AB. Ответ дайте в сантиметрах.

Объяснение:

Серединные перпендикуляры к сторонам треугольника  пересекаются в одной точке — центре описанной окружности.

Значит МА=МВ=МС=R = 14 см.

Тогда ΔАМВ - равнобедренный с основанием АВ  и ∠МАВ=∠МВА=30°.

Расстоянием от т.М до стороны АВ есть высота равнобедренного  ΔАМВ.

Построим высоту МК. Получили прямоугольный ΔВМК с прямым ∠МКВ и гипотенузой МВ.

Катет МК = sin∠MВK * MВ.

Т.к. ∠МВК = ∠АВМ = 30°   и МА = 14 см, то

МК = sin 30° * 14 = 7 (см)