Предмет: Геометрия,
автор: keksik897
ребят помогииите, кто нибудь
Приложения:
Ответы
Автор ответа:
3
Первый способ
Теорема косинусов: для плоского треугольника со сторонами и углом
, противолежащим стороне
, справедливо соотношение:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов:
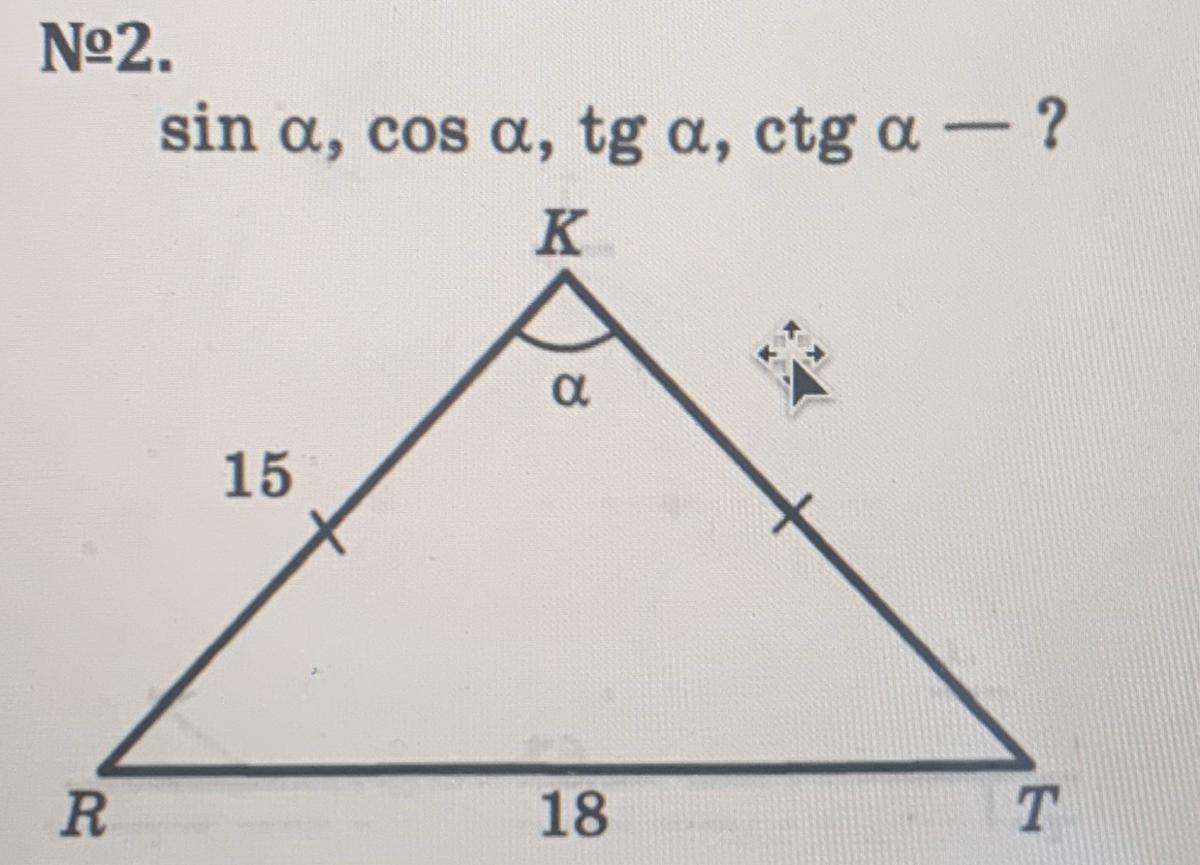
Для заданного треугольника имеем:
Применим основное тригонометрическое тождество:
Выразим из этого тождества синус для острого угла :
Следовательно:
Второй способ
Проведем в равнобедренном треугольнике высоту
, являющаяся медианой и биссектрисой, то есть
и
Рассмотрим прямоугольный треугольник
По теореме Пифагора
Тогда
Применим теорему синусов: стороны треугольника пропорциональны синусам противолежащих углов:
Аналогично:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: katerina9898
Предмет: Русский язык,
автор: rfnz19
Предмет: Другие предметы,
автор: dilechka2005
Предмет: Математика,
автор: Neekita
Предмет: Биология,
автор: tap783012