Предмет: Геометрия,
автор: sofia334702
знайти площу трапеції основи якої дорівнюють 7 і 9 см а бічна сторона довжиною 6 см утворює з більшою основою кут 45°
Ответы
Автор ответа:
72
Відповідь:
24√2 см²
Пояснення:
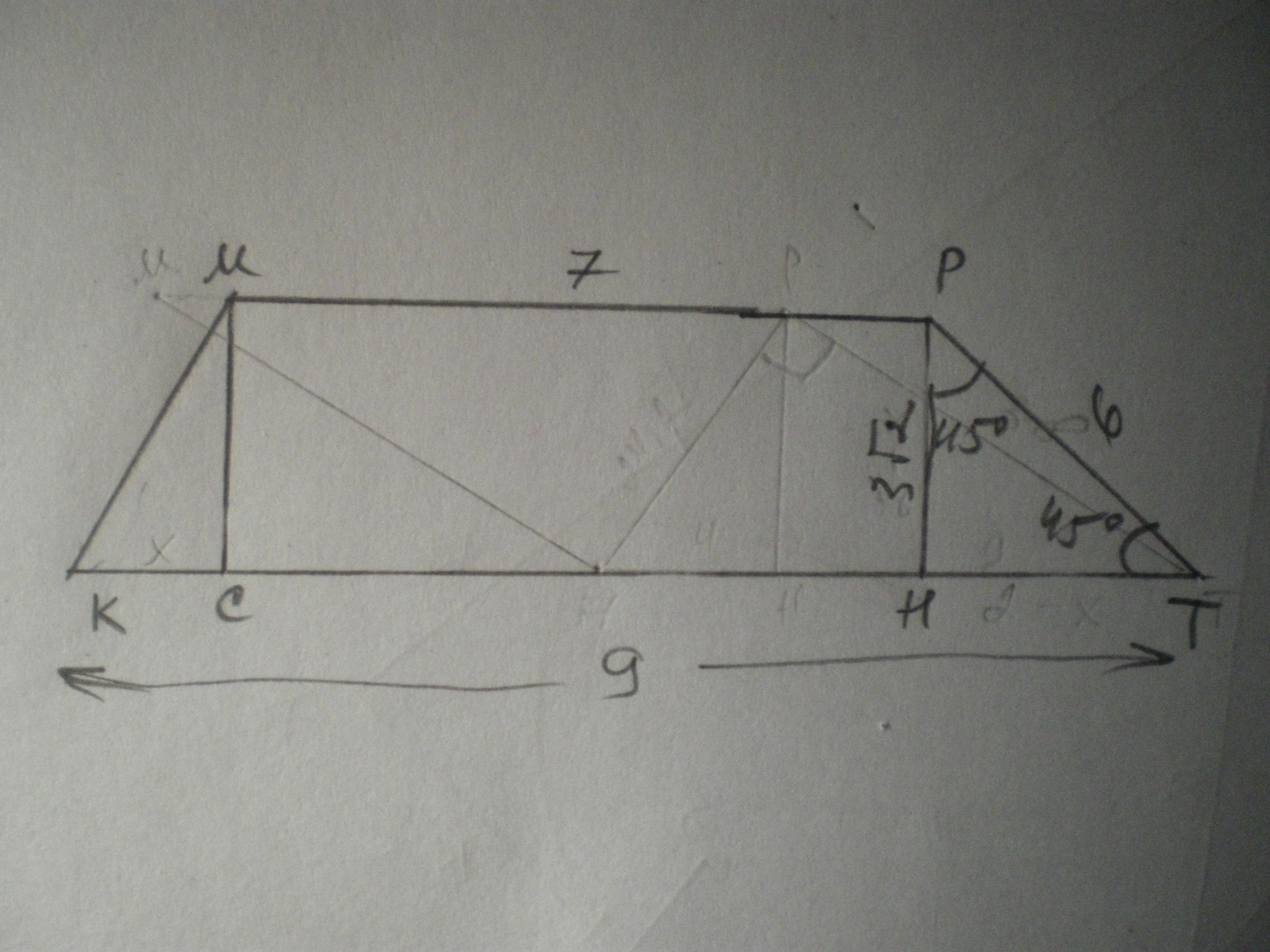
Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kotenok55
Предмет: Русский язык,
автор: elmirazinatyll
Предмет: Русский язык,
автор: Evseevau
Предмет: Алгебра,
автор: maria2711
Предмет: Математика,
автор: jyliapoleno