Question

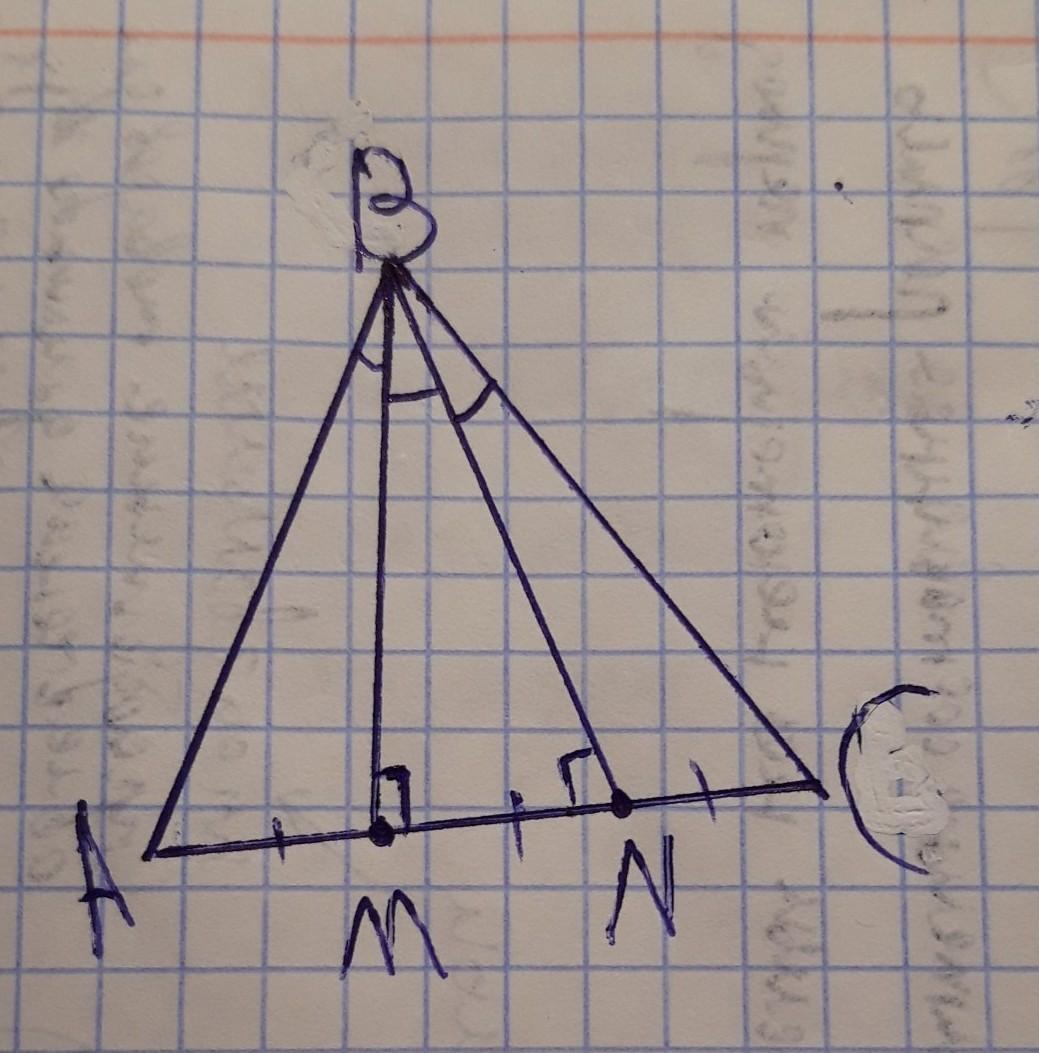
На стороне AC треугольника ΔABC отмечены точки M и N (M принадлежит[AN]). Известно, что AM=MN=NC.
Возможно ли при этом равенство углов ABM=MBN=NBC?
СРОЧНО!!! ПОМОГИТЕ ПОЖАЛУЙСТА

Answer 1

Ответ:

Нет

Допустим, что углы ABM=MBN=NBC

1.Тогда рассмотрим Треугольник АВN:

т.к. угол ABM равен углу MBN, следовательно BM биссектриса. т.к. АМ равен МN следовательно ВМ медиана. ВМ медиана и биссектриса, следовательно треугольник АВN равнобедренный, следовательно ВМ высота, следовательно угол ВМN = 90°.

2. Так же рассмотрим треугольник МВС:

т.к. угол CBN равен углу MBN, следовательно BN биссектриса. т.к. NC равен МN следовательно BN медиана. ВN медиана и биссектриса, следовательно треугольник MBC равнобедренный, следовательно ВN высота, следовательно угол BNM = 90°.

3. получается, треугольник BNM - равнобедренный, при основании равные углы по 90°. но такого быть не может, так как сумма углов в треугольнике равна 180°.