Предмет: Математика,
автор: jgjejehehdje
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!
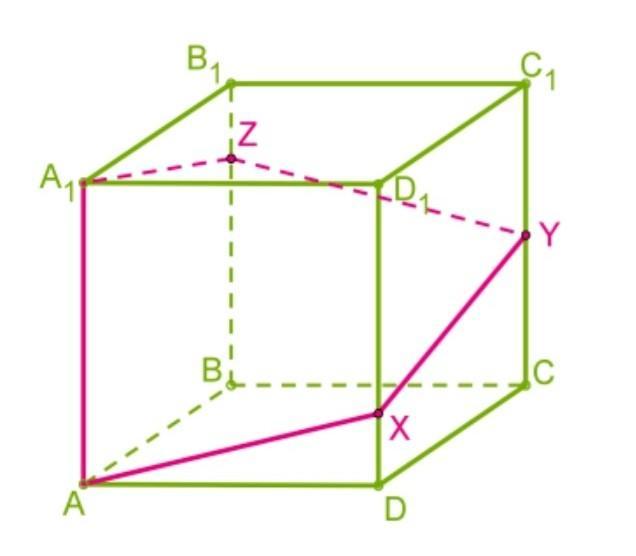
Муравей начинает путешествие по поверхности куба от вершины A и возвращается обратно в вершину A.
Дорога состоит из отрезков. Конечные точки отрезков на рёбрах расположены так, что DX:XD1=1:3;CY:YC1=1:1;BZ:ZB1=3:1.
Определи длину дороги муравья с точностью до сотых, если ребро куба равно 10 см
(все промежуточные вычисление округляй до сотых).
Приложения:
Ответы
Автор ответа:
3
Ответ:
51.2
Пошаговое объяснение:
По теореме Пифагора найдём длину
Аналогично:
Как посчитать длины ? Точка
находится в центре ребра, а
на четвертях. Расстояния между их проекциями также равно 2.5. Следовательно,
.
И в ответе:
Похожие вопросы
Предмет: Русский язык,
автор: kijashko83
Предмет: Русский язык,
автор: kijashko83
Предмет: Русский язык,
автор: platonovanadya
Предмет: История,
автор: Mihatiko
Предмет: Алгебра,
автор: serega01011