В правильной четырехугольной пирамиде все рёбра которой равны 1 точка E середина ребра SC найдите тангенс угла между прямыми SA и BE
Ответы
Ответ:
Tg(SA^BE) = √2.
Объяснение:
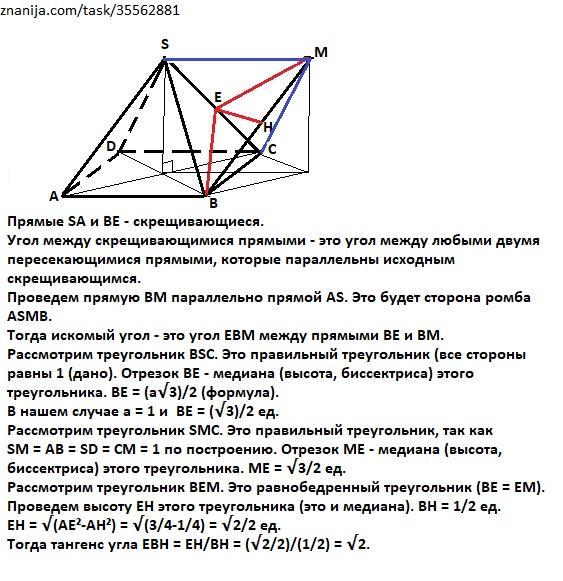
Прямые SА и ВE - скрещивающиеся.
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем прямую ВМ параллельно прямой АS. Это будет сторона ромба ASMB.
Тогда искомый угол - это угол ЕВМ между прямыми ВЕ и ВМ.
Рассмотрим треугольник ВSС. Это правильный треугольник (все стороны равны 1 (дано). Отрезок ВЕ - медиана (высота, биссектриса) этого треугольника. ВЕ = (а√3)/2 (формула).
В нашем случае а = 1 и
ВЕ = (√3)/2 ед.
Рассмотрим треугольник SMС. Это правильный треугольник, так как SM = АВ = SD = СM = 1 по построению. Отрезок МЕ - медиана (высота, биссектриса) этого треугольника.
МЕ = √3/2 ед.
Рассмотрим треугольник ВЕМ. Это равнобедренный треугольник
(ВЕ = ЕМ). Проведем высоту ЕН этого треугольника (это и медиана).
ВН = 1/2 ед.
ЕН = √(АЕ²-АН²) = √(3/4-1/4) = √2/2 ед.
Тангенс угла ЕВН - отношение противолежащего катета к прилежащему.
Tg(∠EBH)= ЕН/ВН = (√2/2)/(1/2) = √2.