Предмет: Математика,
автор: cifej73274
Решите производную сложной функции
Приложения:
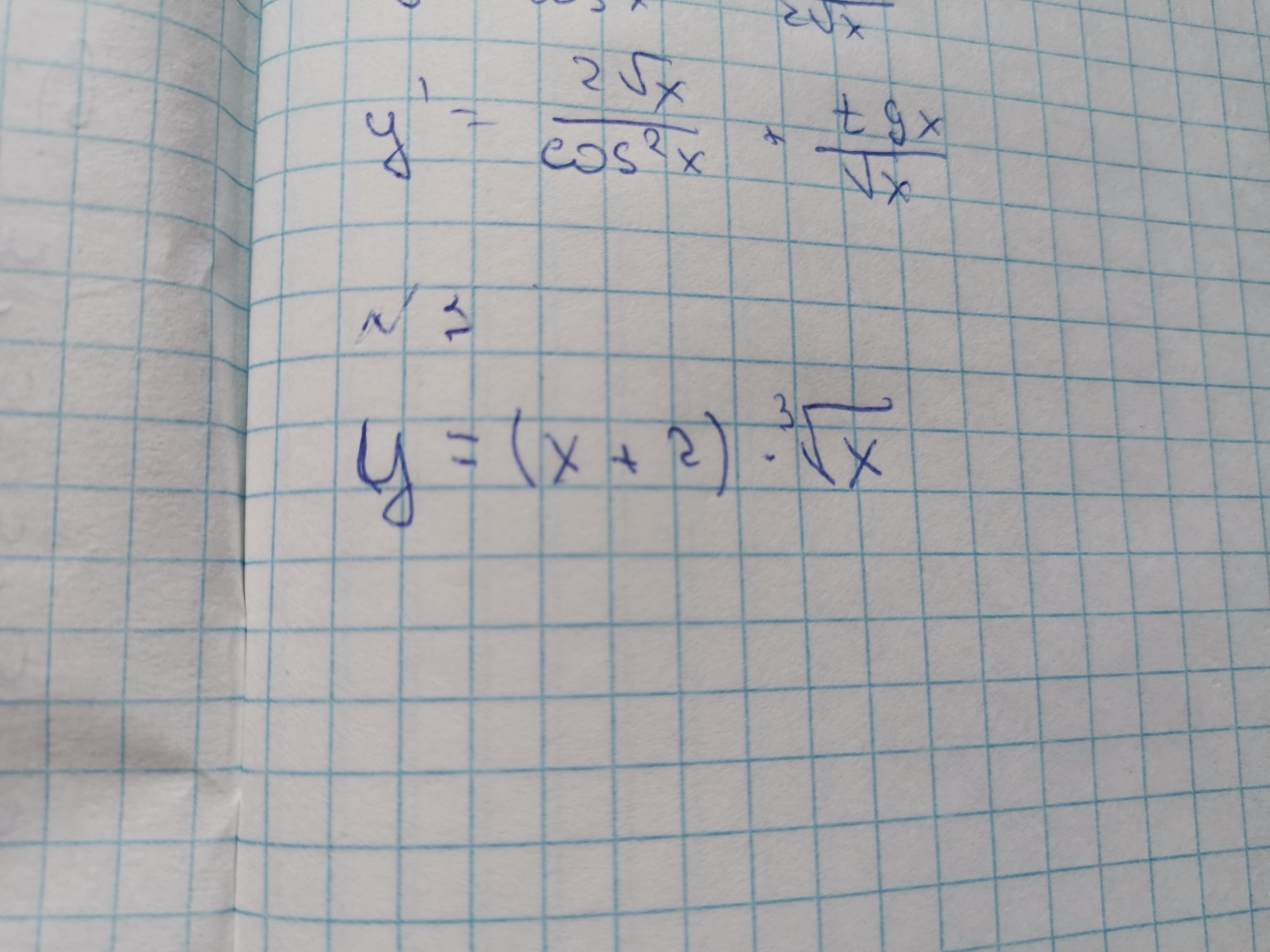
Ответы
Автор ответа:
2
cifej73274:
Спасибо что ты есть
Похожие вопросы
Предмет: Русский язык,
автор: Polinaa99
Предмет: Русский язык,
автор: kioalenka
Предмет: Русский язык,
автор: kioalenka
Предмет: Химия,
автор: kolinyukyulya